3. 선형 결합(Linear Combinations)

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다.

 

선형 결합은 $R^n$ 차원상의 벡터들에 상수 배를 곱해서 전부 더한 것입니다. 선형 결합이 나온 이유는 우리가 푸는 딥러닝 문제들도 입력 데이터에 상수 배(파라미터)를 곱하는 형태이기 때문입니다.

 

 

예제를 coulmn vector로 보면 $R^3$에 속하는 선형 결합으로 볼 수 있습니다. 그러면 다음과 같이 방정식 형태로 나오게 되는데 이것을 벡터 방정식이라고 합니다.

 

 

Span

어떤 벡터들의 모든 선형 결합의 결과물을 모은 것이 Span입니다. 유한한 재료 벡터들을 가지고 만들 수 있는 모든 선형 벡터의 집합입니다. span은 하나의 실수 공간을 만들 수 있습니다. 연립 방정식이 아닌 벡터 방정식을 통해서 문제에 접근해보겠습니다. 이 벡터 방정식의 span으로 $[60, 74, 78]^T$을 표현할 수 있으면 해가 존재하고 span으로 표현할 수 없으면 해가 없다고 합니다. 벡터 방정식에서 미지수의 개수는 열벡터의 개수이고 방정식은 벡터들이 살고 있는 전체 집합의 차원입니다.

 

 

- 행렬곱 하는 방법

 

 

하나의 row와 column의 선형 결합으로 표현 가능합니다. 

 

 

이런 행렬을 3개의 재료 벡터로 보고 곱해지는 열 벡터를 3개의 가중치로 생각하고 연산을 진행하면 됩니다. 

 

 

Sum of (Rank-1) Outer Products (외적)

외적은 열벡터, 행 벡터 순서로 연산을 하는 것인데 행렬에서도 외적이 사용됩니다. 일반적인 외적은 하나의 벡터로 이루어지고 외적의 결과물로 행렬이 나오게 됩니다. 

 

 

하지만 행렬들도 보는 관점에 따라 외적을 표현할 수 있습니다. 여러 개의 벡터로 나눠서 진행하면 됩니다.

 

 

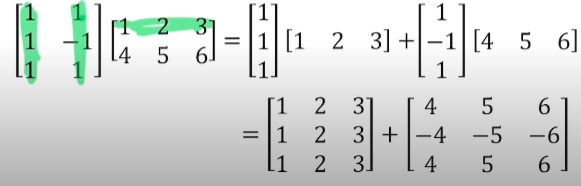
중간 단계에서 벡터들끼리 외적을 해서 행렬이 2개 생성되었고 이 두 개를 더하는 방식으로 진행이 됩니다. 만약 행렬이 아니라 scalar값이 나온다면 내적으로 생각하면 됩니다. 위 사진과 같은 방법으로 행렬을 벡터의 연산으로 근사하여 표현할 수 있습니다. 이런 경우 더 적은 데이터로 표현할 수 있게 됩니다.