Convolution Network을 학습할 때 ImageNet의 도움을 받을 수 있습니다. ImageNet의 가중치를 가져와서 우리 모델에 적용하는 것이 Transfer learning 입니다. (이후에 우리의 문제에 알맞게 fine tuning을 진행하면 됩니다.)

다음과 같이 fine tuning을 어느 정도할 것인지 정할 수 있습니다.
- 만약 가지고 있는 데이터가 너무 적다면 나머지 부분은 고정시키고 classfier 부분만 훈련시킵니다.
- 데이터가 어느 정도 있다면 ImageNet 가중치를 가져와 모델의 초기값으로 사용합니다.
이제 Nerual Netowrk에 역사에 대해 알아보겠습니다.
Neural Netowrk의 발전
초기에는 단순한 연산만을 할 수 있는 perceptron 으로 시작합니다.

Perceptron과 Neural Network의 차이점은 activation function에 있습니다. Perceptron의 경우 activation function이 단순한 binary function이기 때문에 back propagation, gradient descent를 사용할 수 없습니다. binary function은 기울기가 없기 때문에 직접 가중치들을 조작하면서 최적의 값을 찾아갔습니다.
Perceptron으로는 단순한 AND, OR 등의 문제들만 해결할 수 있었고 XOR 문제는 해결할 수 없었습니다. 그렇기 때문에 연구가 진행되었고 그 다음으로 나온 것이 Perceptron을 쌓아 올린 Multi layer perceptron 입니다.
그 다음으로 나온 것이 최초의 back propagation이 등장하게 됩니다.

미분이 가능하고 back propagation도 가능해서 최적의 파라미터를 체계적으로 찾아갈 수 있을 것 같았지만 layer가 깊어질 수록 제대로 동작하지 못했습니다.
back propagation을 잘 동작시키기 위해서 RBM이라는 개념이 도입되게 됩니다.

여러 묶음의 RBM으로 선행학습을 진행한 후 두 번째로 이 묶음들을 하나로 만들어 실행시켰더니 잘 동작 되었다고 합니다. 마지막 3단계에서는 fine tuning을 진행합니다.
- 나중에는 back propagation 동작에 이상이 있던 이유는 weight initialization 방법과 sigmoid function 에 의한 문제였기 때문에 굳이 RBM 개념을 적용하지 않아도 해결이 가능해졌습니다.
이제 CNN이 등장합니다. 제대로된 weight initialization과 activation function을 적용할 수 있었고 GPU의 성능 증가와 데이터의 증가로 인해서 활발하게 발전되기 시작합니다.
Activation function

다음과 같이 노드에서 나오는 단순한 Linear한 합에 non - Linearity를 적용한 것입니다. sigmoid function을 통해서 최종적으로 확률적인 값을 얻을 수 있었습니다.
- 들어오는 입력에 대한 가중치에 영향을 주기 좋은 형태여서 많이 사용했지만 뉴런이 포화되서 gradient vanishing 문제가 있었습니다.

gradient vanishing의 원인은 sigmoid의 입력 x가 매우 큰 값을 가지게 된다면 이때 x에 대한 sigmoid의 변화율을 구하면 기울기가 거의 0에 가까운 값이 나옵니다. 입력 x가 작을 때도 마찬가지 입니다.
- 즉 x의 값이 꽤 작거나 꽤 큰 경우에는 local gradient가 0이 되는 현상이 발생되게 됩니다.
- sigmoid의 기울기가 크게 존재하는 부분을 active region of sigmoid라고 합니다. (0 주변 영역)
- 양쪽 끝 부분은 saturated region = 포화지점 = 더 이상 얻을 기울기가 없다.
그리고 또 다른 문제점으로 sigmoid function의 중심이 0이 아니란 것입니다. (y = 0.5가 중심)
그 결과 computation이 매우 느려집니다.
이유 = 가중치의 기울기가 모두 양수이거나 음수여야함
- $f(\Sigma w_i \times x_i +b)$를 $w$로 미분할 때
- $ \frac {df}{dw_i} = x_i$ 미분시 $x_i$는 무조건 양수
- $\frac {dl}{dw_i} = \frac {dl}{df} \times \frac {df}{dwi} = \frac {dl}{df} \times x_i$
최종 결과가 $ \frac {dl} {dw_i} = \frac {dl}{df} \times x_i$ 인데 $x_i$는 시그모이드 값으로 항상 양수 입니다.
즉 ${dl} {dw_i}$ 는 $\frac {dl}{df}$와 항상 같은 부호를 가져야합니다.

- 즉 w의 기울기는 모두 양수거나 모두 음수입니다.
- 위와 같이 w0, w1이 존재할 때
- (1, 1), (-1, -1) 이 방향으로 밖에 못 움직입니다.
그렇기 때문에 가중치를 업데이트할 때 파란색이 최적의 경로일 때 다음과 같이 지그재그로 움직입니다.
마지막 3번째 exp 연산량이 비싸서 느립니다.
- 저는 시그모이드 출력값이 어떠한 경우에도 0이 되지 않는 것을 보고 0이 아니니까 연산이 이루어져 더 느려진다 라고 생각했습니다.
지금 설명드릴 activation function들은 sigmoid의 문제점을 해결한 function들 입니다.
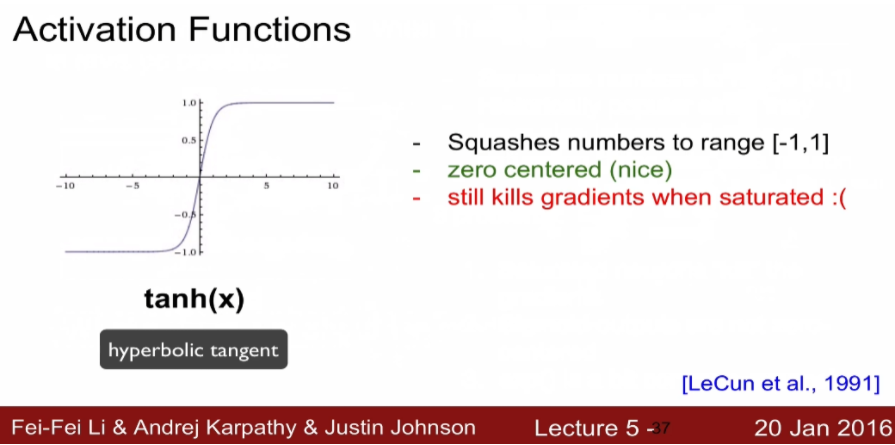
tanh는 중심 값을 0으로 만들어 어느 정도 문제는 해결했지만 아직도 gradient vanishing이 존재합니다.
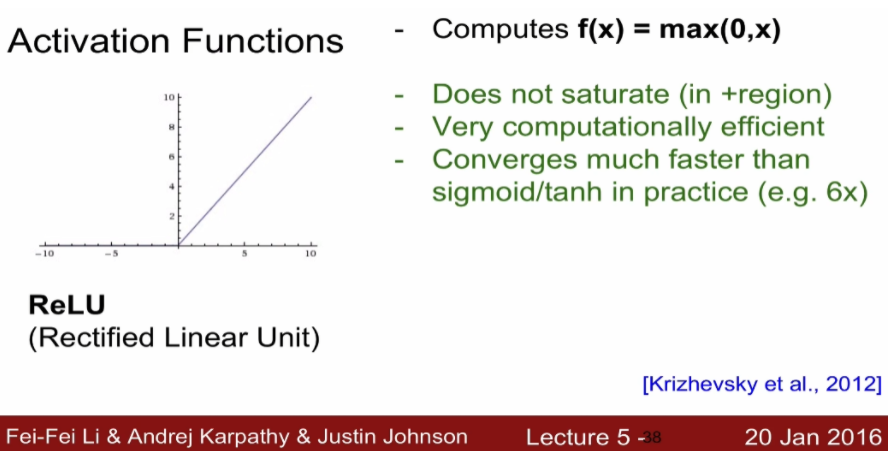
기본 활성화 함수, 연산이 매우 효율적이고 시그모이드나 쌍곡탄젠트보다 6배 빠르다고 합니다.
- 출력값의 중심이 0이 아닙니다. = not zero-centered output
- 입력이 0보다 작을 때 기울기가 0이 되는 문제점이 존재
- ReLU가 기본 설정 함수이긴 하지만 문제점을 알아야 나중에 능동적으로 설정할 수 있다

Dead ReLU 개념
- 뉴런이 데이터 클라우드(데이터가 들어가는 부분) 내에 있는 경우 = active ReLU
- 외부에 있을 경우 DeadReLU = 운이 나빠서 초기값이 Dead ReLU zone에 있을 때, 학습을 시킬 때 Learning rate가 너무 클 때
- 저렇게 데이터 밖으로 나가게 되면 다시는 안으로 들어오는 경우도 많습니다. = 업데이트가 제대로 진행이 안됨 = 활성화 함수 입력값이 0으로 들어가서 입력들이 전부다 죽어버리는 것 = 기울기가 0이 되니 학습이 안되는 것
- 이런 문제를 해결하기 위해서 뉴런을 초기화 할 때 바이어스 값을 0.01 정도로 아주 작은 양수 값으로 초기화 합니다.
- 이렇게 하면 음수가 아니라서 기울기가 살 수 있기 때문
이러한 문제점을 해결한 것이 Leaky ReLU입니다.

0보다 작을 때 기울기가 0이 되는 것이 아니라 기울기를 가지는 형태를 가집니다. x가 0보다 작을 때도 saturation이 되지 않습니다.
기본적으로 ReLU를 사용하고 연구나 실험을 하는 경우 Leaky ReLU나 maxout을 사용합니다.
tanh이나 sigmoid는 LSTM에서는 아직 사용합니다.
Preprocess the data

오리지널 데이터가 존재할 때 우선 zero center를 맞춰주고 각각에 대해서 전체의 평균 값을 빼주면 됩니다.
- 그 다음 분산을 줄이기 위해서 정규화를 해줍니다.
- 이미지는 기본적으로 0~255 사이 값을 가져서 잘 정규화 안한다고 하지만 실제로는 0~1 값으로 자주 해줍니다.
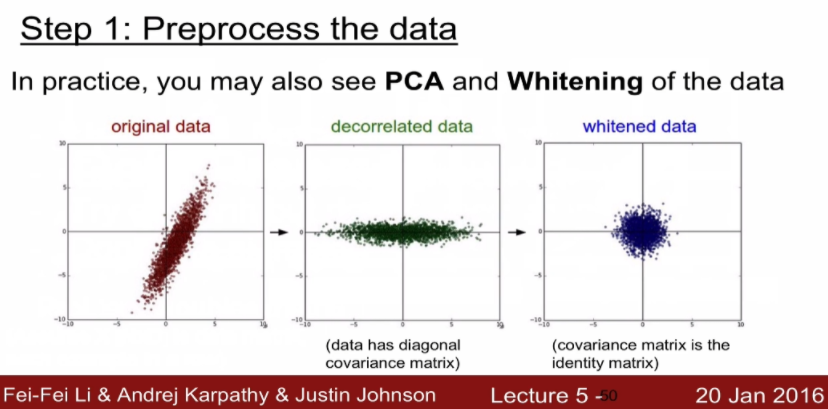
PCA는 데이터를 비상관해서 차원을 줄이는 것이고 whitening은 이미지에 인접하는 픽셀간의 redundancy 줄여질 수 있도록 squashing 해주는 역할을 합니다. 이미지에서는 큰 의미가 없다고 합니다.
- 이미지는 zero center들에만 신경 써주면 된다고 합니다.
Weight inigialization
모든 가중치가 0으로 초기화되면 모든 뉴런들이 동일한 연산을 수행하고 역전파도 동일한 연산을 진행하여 symmetry breaking(대칭 깨짐)이 발생하지 않습니다. (모든 신호의 중요도가 비슷하게 평가된다는 의미입니다.)
1. small random number
- random number를 사용하는데 매우 작은 수를 사용
가장 좋은 방법은 랜덤으로 초기화입니다. 첫번째 방법은 매우 작은 수로 진행하는 방법입니다. 그래서 0을 평균으로 가지고 0.01표준 편차를 가지는 가우시안 정규 분포로 구성합니다.
이렇게 구성을 하면 네트워크가 작은 경우에는 괜찮지만 네트워크가 커지면 활성화 값이 가운데로 쏠리는 형상이 발생 = 모든 활성화 값들이 0이 되버립니다.
w = 0.01 * random.random(D, H)역전파를 할 때 기울기는 $dw1 = x \times dw$로 모든 활성화 값이 0에 가깝게 가버리니까 $dw1$도 작아지게 되면서 기울기가 소실되게 됩니다.
0.01 대신 1을 줄 경우 overshooting으로 인하여 모든 뉴런들이 saturation이 되서 -1, 1에 포화됩니다.
- 초기 가중치 값이 너무 커서 그냥 기울기가 0이 나오는 지점으로 이동합니다. (보폭이 너무 크다)
- 학습을 시킬 때 loss 값이 전혀 변하지 않으면 초기 가중치 값이 너무 크게 잡아서 입니다. (loss 값이 진동할 때도 이 문제일 확률이 높습니다.)
2. Xavier initialization
가중치 값을 input 개수로 나눠서 input 개수가 크면 가중치가 작아지고 적으면 가중치가 커지는 방식입니다.
- saturation이 일어나지 않고 잘 학습이 진행됩니다.
- tanh 같은 함수에 잘 적용되지만 ReLU에서는 문제가 발생합니다.
W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in) # input 개수에 제곱근을 해준 상태W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in / 2) # ReLU 문제를 해결할려면 2로 나눠주면 됩니다.
초기값 선택이나 초기화 방법이 너무 복잡했기 때문에 이러한 문제를 해결하기 위한 방법으로 batch normalization이 나오게 됩니다.

gradient vanishing이 일어나지 않게 해주는 방법으로 이전까지는 gradient vanishing을 막기 위해서 activation function을 변형시키거나 weight initialization을 신중하게 선택해야하는 번거로움이 있었습니다. batch normalization은 layer를 거칠 때 마다 분포가 바뀌는 문제로 인해서 기울기가 소실되는 문제가 생긴다고 생각했고 다음과 같이 각 레이어를 거칠 때 마다 normalization을 해주는 방법을 도입합니다.
- normalization을 해도 미분이 가능한 값들이라서 Forward Propagation이나 Backward Propagation에 아무 문제가 없기 때문에 그냥 적용해서 사용하면 됩니다.
'cs231n' 카테고리의 다른 글
| 3. Backpropagation and Neural Networks part 1 (0) | 2021.10.12 |
|---|---|
| 2. Loss function and Optimization (0) | 2021.10.11 |
| 1. Image classification (0) | 2021.09.19 |