1. convex optimization 란?

 

 

최적화를 공부해야하는 이유는? 

 

- 어떤 변수가 존재하고 그 변수에 따른 비용이 존재할 때, 비용을 최저로 줄이는 변수를 찾을 수 있습니다. (효율적이다!)

 

지금 공부할 convex optimization은 convex 형태의 최적화 문제를 푸는 방법입니다.

 

 

convex optimization에는 inequality와 equality라는 조건이 존재합니다. 이 조건들이 만족하는 범위내에서의 변수 중 가장 낮은 cost를 갖는 변수를 찾아야 합니다.

 

우리가 최적화할 함수를 표현할 때는 $min$ $f(x)$로 표현하고 object function이라고 부릅니다. 그리고 minimize할 때 제한 조건들(constraints)은 다음과 같습니다.

 

1. $subject$ $to$ $h(x)=0$  (equality)

2. $subject$ $to$ $g(x)\le 0$ (inequality)

 

 

조금 간단하게 벽지를 사는 문제로 예시를 들어보겠습니다. 벽지를 살 때 간단하게 2가지 조건이 붙는데

• 첫 번째는 벽과 벽지의 크기가 같아야합니다. (equality)
• 두 번째는 예상한 금액 안에서 해결해야합니다. (inequality) 

여기서는 cost는 variable이 되고 variable은 벽지의 종류가 될 것입니다. 우선 벽에 딱 맞는 벽지들 중에서 가격을 비교하여 예산안에 들어오는 벽지들을 찾아야합니다. 조건들을 충족하는 선택지를 feasible solution 이라고 합니다. 이때 조건을 충족하는 선택지가 여러 개가 존재할 수 있습니다. 이 feasible solution들을 모아서 feasible set이라고 부릅니다.

 

조건을 만족하는 선택지 중 가장 적은 비용의 선택지를 optimal solution이라고 합니다.

 

- feasible set에 포함되면서 cost를 최소화 시켜주는 solution이 optimal solution

 

 

 

Convex optimizaiton problem의 정의

 

convex optimizaiton problem이 되기 위해서는 object function $f(x)$가 convex이고 feasible set이 convex여야 합니다.

feasible set이 convex하다는 건 어떤 걸까요?

 

위키백과 - 볼록집합

 

feasible set이 convex하기 위해서는 사진의 첫 번째 집합과 같아야 합니다. 즉 집합에 존재하는 점과 점을 이었을 때 그 선분도 집합에 포함되어야 합니다. 

 

즉 set에 존재하는 모든 $x$, $y$에 대해서 $\alpha x+(1-\alpha )y$도 set에 포함되어야 한다는 것입니다. ($x$, $y$는 set에 존재하는 임의의 점)

 

$x-y$ 같은 경우

 

 

 

다음과 같은 벡터가 만들어집니다. 그리고 여기다 $\alpha$를 얼마나 곱하냐에 따라 길이가 달라지게 됩니다. 이렇게 만들어진 벡터의 모든 경우가 set에 들어가야합니다. ($\alpha$는 0~1 사이 값입니다.)

 

이제 convex function에 대해서 알아보겠습니다.

 

 

 

Convex function

 

convex set은 두 점 사이의 점들이 set안에 존재한다는 조건을 만족시키면 됬었습니다.

그럼 convex function은 어떨까요?

 

마찬가지로 함수위에 임의의 두 점을 고르고 그 사이를 선으로 이었을 때 함수값들이 선보다 아래 존재하면 됩니다. 이 선분은 $\alpha f(x_1)+(1-\alpha )f(x_2)$가 되어서 이 값보다 작으면 됩니다.

 

$f(\alpha x_1+(1-\alpha )x_2\le \alpha f(x_1)+(1-\alpha )f(x_2)$ 조건을 만족하면 사진과 같은 함수가 나옵니다.

 

다음과 같이 선분보다 작으면 됩니다.

 

convex한 경우 모든 구간에서 미분이 가능한데 이때 두 번 미분하면 양수가 나오게 됩니다. 만약 두 번 미분했을 때 행렬이 만들어진다면 그 행렬이 positive definite matrix가 됩니다.

 

이렇게 feasible set이 convex하고 object function이 convex할 때 convex optimizaiton problem이라고 합니다. convex optimizaiton problem은 local minimum이 optimal solution이 되기 때문에 간단하게 문제를 해결할 수 있습니다.

 

만약 convex optimization problem에서 local minimum을 찾았는데 이 local minimum보다 작은 것이 있다면 그것은 local minimum이 아닙니다. 주변에 더 작은 값이 존재하는 것이기 때문입니다. 

 

왜 전 구간 convex여야만 convex problem일까?

 

 

 

 

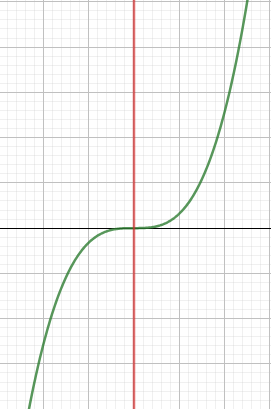
사진 속 함수는 전 구간 convex하지는 않지만 부분적으로 convex합니다. ($x\ge 1$에서는 convex 합니다.)

이렇게 된 경우 initialize 과정에서 convex하지 않은 바깥 부분에서는 초기화 할 때 최적화하기가 어려워집니다.