- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다.
subspace는 부분공간, 부분집합으로 생각하시면 됩니다. span과 유사한 개념입니다. $R^3$같은 3차원 실수 공간은 3차원 벡터를 전부 모아둔 곳이고 이곳의 일부 벡터를 가지고 있는 것들이 부분 집합, subsapce입니다.
supspace의 요소로 basis가 나옵니다. subspace를 전부 표현할 수 있는 벡터들을 basis라고 부릅니다. 즉 subspace의 재료벡터이면서 선형결합으로 subspace의 모든 벡터를 표현할 수 있다는 의미입니다. 하지만 선택된 재료벡터는 선형독립이여야 합니다.
Find a basis
기저벡터(basis)는 unique하지 않기 때문에 한 subspace에 여러 개가 존재합니다. 서로 다른 기저벡터를 사용해 같은 점을 표현해본다면 벡터들에 사용되는 가중치값이 달라집니다.

이 점을 다른 기저벡터로 표현해본다면

subspace에서 기저벡터는 unique하지 않지만 dimension은 unique 합니다. dimension은 기저벡터의 개수를 의미합니다.
- 기저벡터의 개수란 subspace에서 선형독립을 충족하기 위한 것으로 2차원에서는 2개의 재료벡터를 기저벡터로 사용해야 합니다.
3차원 공간의 기저벡터는 여러 종류가 있겠지만 가장 대표적인 것은 Standard basis입니다.
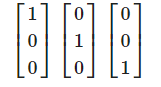
이것을 Standard basis라고 부릅니다. 다음과 같은 column vector들의 span으로 이루어진 것을 column space라고 부릅니다. - $Rank A = dim Col A = $ column spcae의 차원
어떤 task에 대해서 가지는 feature의 개수가 column의 개수가 됩니다. column 개수가 많아도 정보가 적은 경우가 있습니다. 이런 경우는 보통 한 개의 column의 spcan으로 나머지 column을 표현할 수 있을 때입니다. 이런 경우는 여러 개의 coulmn이 존재하더라도 중복되는(span에 포함되는) column들을 전부 제외한 상태로 Rank가 설정이 됩니다.
- feautrue이 많아 보여도 Linear dependent 한 column을 가지는 경우 그 coulmn이 주는 부가적인 정보는 없습니다. 이렇게 중복되는 정보들은 모델을 해집어두면서 overfitting이 일어날 확률을 높입니다.
'수학 > 인공지능을 위한 선형대수' 카테고리의 다른 글
| 7. 선형변환 with Neural Networks (0) | 2021.10.13 |
|---|---|
| 6. 선형변환(Linear transformation) (0) | 2021.10.12 |
| 4. 선형독립과 선형종속 (0) | 2021.10.09 |
| 3. 선형 결합(Linear Combinations) (0) | 2021.09.30 |
| 2. 선형방정식과 선형시스템 (0) | 2021.09.19 |