- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다.
Linear Equation(선형 방정식)
$a_1x_1 + a_2x_2 + ... + a_nx_n $
선형대수에서는 방정식을 한번에 생각할 수 있습니다.
$[a_1, a_2 ... a_3]$
- 일반적으로 Scalar를 표현할 때는 x
- 벡터를 표현할 땐 $x$ (굵게 씁니다.)
- Matrix를 표현할 땐 대문자로 $X$
Linear System: Set of Equations(방정식)
Linear System은 선형 방정식(Linear Equations)의 집합!
- 연립 방정식을 의미합니다.

머신러닝에서도 data, feature의 target label들을 연립 방정식으로 푸는 것과 유사하게 계산합니다. (target label은 정답을 의미 여기서는 수명 Life span)
현 feature(체중, 키, 흡연 여부)의 가중합으로 수명을 잘 예측하는 최적의 계수를 찾는 것이 우리의 목적입니다.

위와 같이 선형식을 만들고 이 모든 선형식에 만족하는 $x_1, x_2, x_3$의 값을 찾는 것이 우리가 연립 방정식을 푸는 방법입니다. 선형대수에서는 일일이 푸는 것이 아닌 vector나 matrix를 통해서 한 번에 직관적으로 나타내 쉽게 이해하려고 합니다. 그래서 다음과 같은 방법으로 문제에 접근합니다.
1. 방정식의 계수들을 전부 모아둡니다.

2. target label값을 벡터로 정의합니다. (등호 뒤에 있는 상수값들)

3. 가중치에 해당하는 값을 벡터화합니다.

이 matrix와 vector을 통해 3개의 연립 방정식을 다음과 같이 $A \times x = b$로 쓸 수 있게 됩니다.

다음과 같이 matrix로 만들었다면 어떻게 연립 방정식을 풀어야 할까요?
1. 역행렬을 사용하여 푼다.
역행렬을 사용하여 풀 때는 Identity Matrix를 사용하여 풉니다. 이것은 항등행렬이라고 하는데 그 이유가 어떤 벡터와 곱해져도 그 벡터 자기 자신을 출력하기 때문입니다.
- $I_nx = x$

항등행렬을 사용하여 역행렬을 구해봅시다. 역행렬은 정사각 행렬만을 대상으로 합니다.(square matrix에만 존재, $R^{n \times n}$)
- 역행렬 정의: square matrix에 대하여 $A^{-1} A = AA^{-1} = I_n$ 교환 법칙이 성립됩니다.
$2 \times 2$에 대한 역행렬은 아래 공식을 사용하여 간단하게 찾을 수 있지만 3차 혹은 그 이상일 경우 이러한 공식은 없지만 차근차근 풀면 풀리는 과정이 존재합니다.
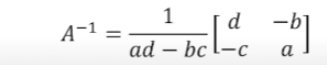
- square하지 않은 matrix는 어떻게 해야 할까요?

이 행렬의 역행렬은 어떤 것인지는 몰라도 지금의 행렬이 (2, 3)이기 때문에 (?, 2) 형태가 나와야 할 것입니다. 여기서 출력으로 나오는 $I$는 정사각 행렬이어야 하므로 (3, 3) 형태가 되어야 하고 교환 법칙이 성립하기 위해서는 ? = 3이 되어야 합니다. - (3, 2) (2, 3)
하지만 (3, 2) shape을 가지고 위에 행렬과 곱했을 때 대각선이 1인 행렬을 찾았다고 해도 역행렬이라고 부르지 않습니다. 역행렬 자체가 sqaure이라는 정의가 붙기 때문입니다. 그리고 sqaure하지 않은 matrix는 웬만해서는 교환 법칙이 성립되지 않습니다.
(2, 3)(3, 2) = (2, 2)에 대한 $I$ 행렬은 만들 수 있지만 일반적으로 (3, 2)(2, 3) = (3, 3)에 대한 $I$는 만들 수 없습니다. - (어떤 법칙이 존재한다고 하는데 자세히는 말씀을 안 해주셨습니다.)
역행렬을 사용하여 푸는 방법은 다음과 같습니다.
$Ax = b$
$A^{-1}Ax = A^{-1}b$
$I_nx = A^{-1}b$
$x = A^{-1}b$
역행렬이 존재하지 않는 경우
역행렬이 존재하면 연립 방정식에서 solution은 unique하게 됩니다. (단 하나의 값) 근이 여러 개 존재하더라도 일일이 대입했을 때 똑같이 identity matrix가 나온다면 그것들은 같은 solution이라고 생각해도 됩니다.
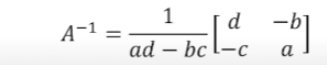
즉 ad = bc, a:b = c:d 비율이 똑같으면 역행렬이 존재하지 않습니다.
$\left [ \begin{matrix} 1 & 2 \\ 2 & 4 \\ \end{matrix} \right] $ 같은 경우 1 : 2 = 2 : 4로 비율이 같습니다.
이 경우에는 연립으로 풀더라도 중립된 방정식들이 끼어들어 있어서 한 변수 (x, y)를 소거할 때 나머지도 같이 소거 되버립니다. 하지만 중복된 방정식 같지만 상수값이 조금 틀어져 있다면 해가 존재하지 않을 수도 있습니다.
여기서 $A = \left [ \begin{matrix} a & b \\ c & d \\ \end{matrix} \right] $ 일 때 $ad - bc$ determinant of A, def A, 판별식이라고 부릅니다.
det A값이 0이 아니면 역행렬이 존재하고 0이면 역행렬은 존재하지 않습니다. 하지만 이것은 $2 \times 2$ matrix에서만 적용되는 판별식으로 이 공식을 사용하면 최적의 파라미터 값을 구할 수 있지만 사용하지 못하는 이유는 애초에 딥러닝이라는 분야에서 $2 \times 2$ matrix보다 훨씬 큰 데이터를 다루기 때문입니다.
- Inverse Matrix Larger than $2 \times 2$: 이 강의에서 $2 \times 2$ 보다 큰 행렬의 역행렬은 어떻게 구하는지 진행되지 않습니다. 혹시 궁금하시다면 Gaussian Elimination을 공부해보시면 됩니다.
Non - Invertible Matrix A for Ax = b
역행렬이 존재하면 solution이 unique하게 하나만 존재하는데 역행렬이 존재하지 않는다면 solution이 무수히 많거나 하나도 없는 상황입니다.
1. 해가 무수히 많은 경우
위에 있는 비율이 같은 matrix를 가져와서 연립 방정식으로 풀면 됩니다.
$\left [ \begin{matrix} 1 & 2 \\ 2 & 4 \\ \end{matrix} \right] $ $\left [ \begin{matrix} x \\ y \\ \end{matrix} \right] =$ $\left [ \begin{matrix} 3 \\ 6 \\ \end{matrix} \right] $
$x + 2y = 3$
$2x + 4 = 6$
첫 번째 식에다 2를 곱해주면 두 번째 식이 나옵니다. 각 식의 형태는 달라보이지만 닫혀있는 형태(Linear dependent), 하나의 식만 존재하는 경우입니다. 이 경우에는 어떻게 접근하던지 자기 자신을 빼는 것이라 0이 나옵니다.
$0x + 0y = 0$
이런 경우 해가 무수히 많습니다. x와 y에 어떤 값을 넣어도 성립되는 조건이기 때문입니다.
2. 해가 없는 경우
$\left [ \begin{matrix} 1 & 2 \\ 2 & 4 \\ \end{matrix} \right] $ $\left [ \begin{matrix} x \\ y \\ \end{matrix} \right] =$ $\left [ \begin{matrix} 3 \\ 7 \\ \end{matrix} \right] $
$x + 2y = 3$
$2x + 4y = 7$
첫 번째 식에 2를 곱해서 빼면 $0x + 0y = 1$이 나오게 됩니다. 이 경우 두 가지 식을 만족하는 x, y 값이 존재하지 않게 됩니다. (이런 경우 오차를 가장 적게해주는 값을 찾아줘야합니다.)
3. Rectangular Matrix
위에서 사용한 예제는 행, 열을 맞춰서 사용했지만 만약 feature 값이 더 많아진다면 나오는 방정식에 비해 미지수가 더 많은 형태가 됩니다.

즉 방정식이 2개 밖에 없는데 미지수가 3개인 상황이라면 일단 해가 무수히 많다고 할 수 있습니다. (dimension 수에 비해서 vetor가 많이 존재한다?)
미지수보다 방정식이 더 많은 경우에는 보통 해가 존재하지 않습니다. 정확하게는 모든 방정식을 만족시키는 해가 존재하지 않습니다. 이런 경우 under-determined system, over-determined system이라고 부릅니다. 하지만 머신러닝이나 딥러닝에서는 해가 없더라도 가장 근사적으로 만족시킬 수 있는 경우를 찾습니다.
만약 미지수가 더 많은 형태로 해가 무수히 많다면 딥러닝, 머신러닝에서는 Regularization을 수행합니다. 이 식을 만족시키는 어떤 점이라도 solution이 될 수 있는데 그 경우에는 변수에 부여하는 가중치를 가장 작게 하는 것이 가장 안전한 solution이 됩니다. 만약 (weight parameter, height parameter) 일 때 (1, 1)과 (5, -1) 이렇게 두 가지 solution이 존재한다면 (1, 1)이 더 안전한 가중치가 됩니다.
- (5, -1)과 (1, 1)이 학습 데이터에서 동일한 성능을 낸다고 하더라도 몸무게에 너무 큰 영향을 받는 모델이라서 안전하지 않기 때문입니다. (정규화를 해서 solution이 무수히 많을 때 커버를 할 수 있습니다.)
'수학 > 인공지능을 위한 선형대수' 카테고리의 다른 글
| 6. 선형변환(Linear transformation) (0) | 2021.10.12 |
|---|---|
| 5. 부분공간의 기저와 차원 (Span and Subspace) (0) | 2021.10.11 |
| 4. 선형독립과 선형종속 (0) | 2021.10.09 |
| 3. 선형 결합(Linear Combinations) (0) | 2021.09.30 |
| 1. 선형대수의 기초 (0) | 2021.08.22 |