이번 강의에서는 방정식의 개수가 미지수의 개수보다 많은 경우에 해결하는 방법에 대해서 이야기해줍니다.

다음과 같이 x를 근사하여 b값 차이(Error)를 구한 다음에 이 값들을 제곱의 합으로 나타냅니다.

제곱의 합이 적을수록 더 좋은 근삿값이 됩니다. 이러한 과정을 요약하자면 $\hat {x} = arg \min \limits_{x} \| b - Ax \|$가 됩니다. 최적의 x값 $\hat {x}$은 $b - Ax$ 값을 최소화시켜주는 x라는 의미입니다.
- L2 norm을 최소화해주는 값을 찾는다.
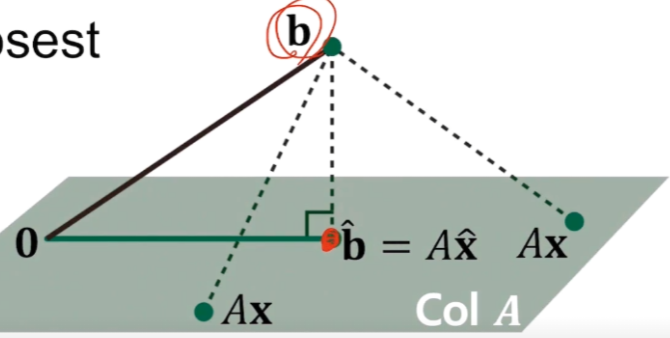
이렇게 근사하는 방법은 b가 A의 span에 포함되지 않을 때 b를 A의 span 평면에 orthogonal projection 한 값을 찾는 것입니다. - 이렇게 하면 A가 이루는 평면에서 b값과 가장 근사한 값을 찾을 수 있습니다.
다음과 같이 삼각형을 만들었을 때 수직이 되어야 하고 b 바로 아래 존재해야 합니다. (수선의 발을 내렸을 때 점)
그리고 점 b와 b hat으로 이루어지는 선이 A행렬의 구성 벡터인 재료벡터들과 수직을 이루어야 합니다.
여기서 A행렬의 재료 벡터들을 $a_1, a_2, ~ a_m$이라고 할 때
- $a^T_1 (b - Ax_{hat}) = 0 $
- $a^T_2 (b - Ax_{hat}) = 0 $
- $a^T_m (b - Ax_{hat}) = 0 $
다음과 같이 내적을 했을 때 0이라는 조건을 만족해야 합니다. 이때 선형결합 내적은 분배 법칙을 따르므로 먼저 곱한 것이 수직이면 나중에 다른 선형 변환이 일어난다고 하더라도 수직이 유지가 됩니다.
$A^T (b - A \hat{x}) = 0$
$A^Tb - A^TA \hat {x}$
'수학 > 인공지능을 위한 선형대수' 카테고리의 다른 글
| 12. Orthogonal Projection 1 (0) | 2021.11.13 |
|---|---|
| 11. 정규 방정식(Normal equation) (0) | 2021.11.10 |
| 9. Least Squares Problem 소개 (0) | 2021.10.17 |
| 8. ONTO and ONE - TO - ONE (0) | 2021.10.15 |
| 7. 선형변환 with Neural Networks (0) | 2021.10.13 |