12. Orthogonal Projection 1

Orthogonal Projection은 $Ax = b$에서 b를 만족시키는 x를 구하지 못했을 때 근사한 $\hat {x}$로 $\hat{b}$을 구하기 위해서 사용됩니다.

 

이것을 행렬 곱으로 표현한다면 다음과 같습니다.

- $\hat{b} = f(b) = A \hat{x} = A(A^TA)^{-1} A^Tb$ 

 

즉 $A(A^TA)^{-1} A^T$을 $b$에 곱해서 Orthogonal Projection의 위치를 알아내는 것입니다. 

 

 

주어진 차원에 벡터가 존재하고 그 벡터끼리 내적을 했을 때 전부 0이 나오면 그것을 Orthogonal set이라고 합니다.

즉 얻어낸 벡터가 전부 수직이라는 것입니다. 비슷하게 Orthonormal set 도 존재하는데 이것은 Orthogonal set에서 한 가지 조건을 더 추가해준 것을 말합니다.

 

3개의 벡터가 수직인 상태에서 길이가 1이 되면 Orhonormal set이 됩니다. 이 Orthonormal set, Orthogonal set은 Linear independent set과 관련이 있습니다. 만약 어떤 벡터 3개가 Orthogonal set이라면 이 벡터는 선형 독립이 됩니다.

 

• Linear independent는 차원이 다른 벡터들로 각도와 상관없이 구성하면 되지만 Orthogonal set은 그 벡터들의 각도가 전부 수직이여야 합니다.
• 머신러닝에서는 수직은 겹치는 정보가 없다는 것을 나타내줍니다.

 

 

Orthogonalization (수직화)

 

 

Orthogonalization을 하는 방법은 서로 수직이 아닌 두 벡터가 존재할 때 

 

 

다음과 같이 수선의 발을 내린 벡터를 구한 다음 그 벡터를 이용한 연산으로 아래 벡터와 수직이 되도록 해줍니다. 수선의 발을 내려 구한 벡터 $\hat {b}$로 $v_2 - \hat{b}$을 통해서 수직이 되지 않게 하는 성분들을 빼주면 다음과 같이 $b$ 벡터를 구할 수 있게 됩니다.

 

조금 더 자세히 설명해보겠습니다.

 

 

정 사영된 수선의 발로 $\hat{y}$를 구하는 방법은 정사영된 곳의 각도가 90도 이므로

 

 

다음과 같이 직각 삼각형이 만들어집니다. 그다음 $y cos \theta$를 하면 밑변 $\hat{y}$를 구할 수 있습니다. 

여기서 $y$와 $u$의 내적은 $\|y\| \cdot \|u\| cos \theta$ 입니다. u길이만 처리한다면 밑변의 길이를 구할 수 있습니다. 

 

- $\frac {y \ cdot u} {\|u\|}$ 이 값이 정사영 벡터의 길이가 됩니다.

 

이 결과값에 방향도 표현해줘야 합니다. 그래서 u의 방향만 알려주기 위해서 $\frac 1 {\|u\|} \cdat u$이렇게 길이가 1이고 방향이 u인 벡터를 만들어 준 다음 곱해주면 됩니다.

 

- $\hat {y} = \frac {y \cdot u} {\|u\|^2} u$

 

 

 

삼수선의 정리로 평면의 orthogonal basis에 각각 orthogonal projection을 한 뒤 그 벡터들을 합치면 해당 평면의 orthogonal projection이 나오게 됩니다. (따로따로 projection 했을 때와 한 번에 했을 때가 같다.)

 

- 삼수선의 정리: 세 가지의 수선인 요소가 있을 때, 평면이 있고 평면 위에 떠있는 점이 있을 때 2가지의 각도가 수직이면 나머지도 수직이다.

 

 

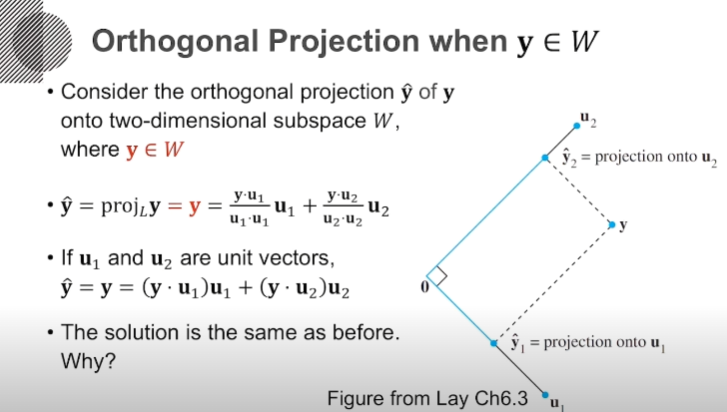
projection 했을 때 얻은 그 점을 포함하는 span $\hat {y}$을 $u_1$, $u_2$으로 표현할 수 있습니다. 이때 $\hat{y_1}$의 각도는 항상 90도여야 합니다.