본 내용은 edwith에서 인공지능을 위한 선형대수 내용 통해 작성되었습니다.
선형대수의 기본적 요소
- Scalar
- 하나의 숫자
- 하나의 숫자
- Vector
- 순서가 정해진 array
- 순서가 정해지지 않은 array는 set
- Matrix
- 행렬, 기본적으로 행렬은 2-dimensional array를 뜻합니다.
- Matrix의 사이즈는 = $row \times column$Row vector의 shape은 (1, n), Coulmn vector의 shape은 (n, 1)의 형태입니다. (Column은 기둥이라는 의미를 가집니다, 세로로 서있는 기둥을 생각하면 조금 더 구분하기 쉬워집니다.)
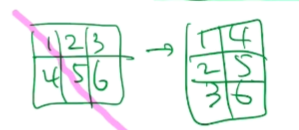
Row vector을 Transpose 하면 Column vector가 나옵니다. Transpose는 아래 사진과 대각선을 중심으로 성분들이 바꿔줍니다.
Matrix Notations
- Square matrix(rows = columns)
- $A \in R^{(n \times n)}$
- Rectangular matrix
(rows $\neq$ columns)- $A \in R^{(m \times n)}$
- Transpose of matrix
- $A^T$ 이렇게 표기합니다.
- 특정 원소를 표현할 때
- $A_{ij}$이것은 (i, j) 행과 열의 인덱스를 의미합니다.
- 덧셈
- 각각의 원소들끼리 더해줍니다.
- 스칼라 곱(상수배)
- 브로드 캐스팅을 해주어 모든 원소에 상수배를 해줍니다.
- Matrix - matrix multiplication
- 왼쪽의 행과 오른쪽의 열을 각각 곱하고 더한 값입니다.
- $(1 \times 2) (2 \times 3)$ 이렇게 열과 행이 맞아야 곱이 가능!
- 내적
- $(1 \times 2) (2 \times 1) = (1 \times 1)$
벡터들로부터 스칼라를 만드는 것
- $(1 \times 2) (2 \times 1) = (1 \times 1)$
- 외적
- $(3 \times 1) (1 \times 3) = (3 \times 3)$
벡터들로부터 행렬을 만드는 것
- $(3 \times 1) (1 \times 3) = (3 \times 3)$
행렬 연산 주의사항!
- $AB \neq BA$ 교환법칙이 성립되지 않습니다. (특수한 경우에는 성립이 될 때도 있습니다.)
- 간단하게 생각하면 매트릭스의 사이즈를 맞춰 연산이 진행되기에 교환을 해버리면 사이즈가 달라지므로 다른 연산이 됩니다.
- 그리고 연산에 순서가 있으므로 교환해버리면 다른 값이 나와버립니다.
다른 법칙
분배법칙 성립
- $A(B + C) = AB + AC$
결합법칙 성립
- $A(BC) = (AB)C$
Property of transpose
- $(AB)^T = B^TA^T$ 이런 성질을 가집니다.
역행렬에서
- $(AB)^{-1} = B^{-1}A^{-1}$
'수학 > 인공지능을 위한 선형대수' 카테고리의 다른 글
| 6. 선형변환(Linear transformation) (0) | 2021.10.12 |
|---|---|
| 5. 부분공간의 기저와 차원 (Span and Subspace) (0) | 2021.10.11 |
| 4. 선형독립과 선형종속 (0) | 2021.10.09 |
| 3. 선형 결합(Linear Combinations) (0) | 2021.09.30 |
| 2. 선형방정식과 선형시스템 (0) | 2021.09.19 |