이번 강의에서는 지난 시간에 배운 새로운 벡터 공간의 개념을 바탕으로 고유벡터와 고유값을 더 이해하고 특성 방정식(Characteristic Equation)을 통해 이들을 구하는 법을 알아봅시다.

Eigenvector와 Eigenvalue를 만족시키는 기본적인 식이 $(A - \lambda I)x = 0$ 입니다. $\lambda$ 정해졌다면 위에 식에 대한 Null space를 찾으면 그것이 $x$입니다.

다음과 같이 $A - \lambda I$를 뺏는데 나온 행렬의 차원을 보면 Row 차원의 벡터들이 중복되어 있어서 벡터들로 만들 수 있는 것은 선 하나입니다. 여기서 Eigenvalue는 3으로 사용했습니다. 3을 사용해서 Lineary independent하게 만들어 줬습니다. 여기서 Row 벡터들의 차원이 총 3차원 중 1차원을 사용했으니 Eigenvactor의 차원은 2차원이 된다는 것입니다.
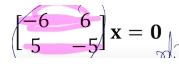
Eigenvalue를 찾는 방법
지금 Eigenvalue를 Diagonal matrix에 곱해서 행렬에 더했을 때 선형종속이 되는 결과가 나왔습니다. 선형종속이 되는 결과가 나왔습니다, 이건 역행렬이 없을 때와 유사합니다. Linear dependent같은 행렬이어야 basis벡터를 찾아 그것을 Eigenvector로 설정해야 되기 때문입니다. 선형 종속의 경우 matrix의 모양과 상관없이 찾을 수가 있는데 역행렬의 경우 square matirx에서만 찾을 수 있습니다. 이것을 Characteristic Equation(특성 방정식)이라고 합니다.

'수학 > 인공지능을 위한 선형대수' 카테고리의 다른 글
| 19. 고유값 분해(Eigendecomposition) (1) | 2022.01.02 |
|---|---|
| 18. 대각화 (Diagonalization) (0) | 2021.12.29 |
| 16. 영공간과 직교여공간 (0) | 2021.11.26 |
| 15. 고유벡터와 고유값 (0) | 2021.11.21 |
| 14. Gram - Schmidt Orthogonalization (0) | 2021.11.18 |