고유값 분해는 주성분 분석(PCA: Principal Component Analysis)에서 자주 쓰이는 개념입니다. 이번 강의에서 고유값 분해를 배우기 위한 첫 단계인 고유 벡터와 고유값의 개념에 대해 배워보도록 하겠습니다.
identity composition
- 주어진 행렬에 대해 굉장히 중요한 정보를 추출하는 과정입니다.
- Square matrix의 Eigenvector가 non - zero 적어도 하나의 원소가 아닌 벡터일 때 다음 식을 만족해야 합니다.
$Ax = \lambda x$

다음과 같이$3 \times 3$ square matrix와 3차원 벡터 x의 곱과 스칼라와 x 벡터의 곱이 같아야 합니다. 이러한 조건을 만족시키는 벡터 x를 A 행렬의 Eigenvector라고 합니다. $\lambda$는 Eigenvalue라고 합니다.
- 행렬 연산을 단순화시킨 것

$ \left [ \begin{matrix} 2 & 6 \\ 5 & 3 \end{matrix} \right]$의 Eigenvector는 $ \left [ \begin{matrix} 1 \\ 1 \end{matrix} \right]$
방향은 그대로고 크기가 8배가 됩니다.
$Ax = 8x$
1. $Ax$ 같은 경우는 크기와 방향이 바뀝니다.
2. $\lambda x$ 같은 경우에는 크기만 바뀌게 됩니다.
이때 저 두 조건을 만족시키는 x를 찾아야 합니다. $Ax$를 그냥 사용할 경우에는 행렬곱을 해야 되기 때문에 4번의 곱셈과 2번의 더하기로 총 6번의 연산이 필요하지만 $8x$ 같은 경우네는 2번의 연산밖에 필요하지 않습니다.
- 행렬곱을 스칼라곱으로 바꿔 효율적인 연산을 진행한다.
Eigenvector와 Eigenvalue를 어떻게 구할 것인가?
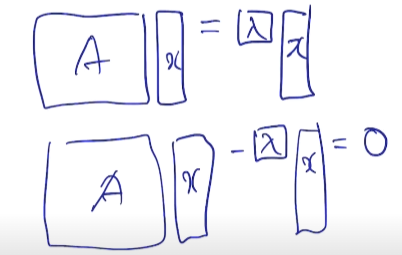
다음과 같이
$Ax = \lambda x$
$Ax - \lambda x = 0$
$Ax - \lambda I x = 0$
$(A - \lambda I)x = 0$
- $I =$ Identity matrix
x에 0을 주면 간단히 해결할 수 있지만 Eigenvector 조건 중에 non - zero vector라는 조건이 있어 0이 될 수는 없습니다. 그래서 영벡터가 아닌 다른 벡터를 넣어주어서 위의 조건을 만족해야 합니다.
$(A - \lambda I)$이건 Linear system으로 볼 수 있습니다. 여기서 행렬 A가 Linear independent 하더라도 $\lambda$를 빼주면 dependent 하게 되도록 해주는 $\lambda$를 찾아야 합니다.

A는 같은 라인에 있지 않아 선형독립이 만족되는 column입니다. 이 행렬에서 대각 성분에만 8을 빼주면 Linear dependent matrix가 나오게 됩니다. 선형종속일 때만 같은 선상에 존재하기 때문에 서로 뺏을 때 0이 나오는 조건을 만족할 수 있습니다.
- 크기는 같고 방향이 반대인 값을 만들어줘야 합니다.
'수학 > 인공지능을 위한 선형대수' 카테고리의 다른 글
| 17. 특성 방정식(Characteristic Equation) (0) | 2021.12.04 |
|---|---|
| 16. 영공간과 직교여공간 (0) | 2021.11.26 |
| 14. Gram - Schmidt Orthogonalization (0) | 2021.11.18 |
| 13. Orthogonal Projection 2 (1) | 2021.11.17 |
| 12. Orthogonal Projection 1 (0) | 2021.11.13 |