1. Linear Algebra

 

다음과 같이 두 개의 미지수를 가진 두 개의 방정식이 존재한다고 해봅시다.

 

 

$2x-y=0$

$-x+2y=3$

 

이 두 방정식을 행렬로 표현한다면 각각의 계수와 미지수를 따로 묶어서 표현합니다.

$$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$

 

방정식의 계수를 모아둔 행렬을 계수 행렬(coefficient matrix)이라고 부르고 $A$로 표기합니다.

그다음 미지수 벡터(the vector of unknown) 를 $x$

마지막으로 이 방정식의 해를 모아둔 벡터를 $b$로 표기해서 선형 방정식 형태로 만듭니다.

- $Ax=b$

 

 

두 방정식을 행렬(system matrix)로 표현했는데 왜 이렇게 표현했을까요?

- 우리의 목표는 방정식을 푸는 것입니다. 방정식을 행렬로 표현할 경우 해를 찾는데 도움이 되기 때문입니다.

 

어떤 식으로 도움이 될까요? 아래 예시를 통해 알아보겠습니다.

 

 

Row picture

- 이 방법은 방정식 형태로 문제를 푸는 것과 동일한 방법입니다.

 

1번째 방정식을 만족시키는 모든 점을 그려봅시다. ($2x-y=0$)

모든 점들이 일직선 상에 있기 때문에 다음과 같이 표현됩니다.

 

 

두 번째 row equation은 원점을 통과하지 않습니다. $-x+2y=3$에서 x와 y에 동시에 0을 집어넣으면 3이라는 결과를 얻을 수 없기 때문입니다.

 

 

방정식들을 만족시키는 점들을 모아 보면 두 방정식을 만족시키는 점을 찾을 수 있습니다.

 

 

여기까지가 row picture로 본 시선입니다. 각각의 연립 방정식을 만족시키는 점들의 집합을 찾아 서로 교차하는 방식입니다. 이제 column picture로 살펴보겠습니다.

 

Column picture

 

column으로 살펴보면 한 번에 두 개의 벡터를 얻습니다.

 

$$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$

 

이 행렬 연산을 다음과 같이 column 벡터와 column 벡터의 덧셈으로 본다면 두 벡터에 적절한 값을 곱해줘 알맞은 선형결합(Linear combination)을 구해야 합니다. 

 

 

- 두 column 벡터에 미지수들이 곱해지는 형태!

$v=x\left[\begin{array}{c}-1\\ 2\end{array}\right]$

 

$u=y\left[\begin{array}{c}2\\ -1\end{array}\right]$

 

여기에 이전에 구한 x = 1, y = 2로 대입해보겠습니다.

 

 

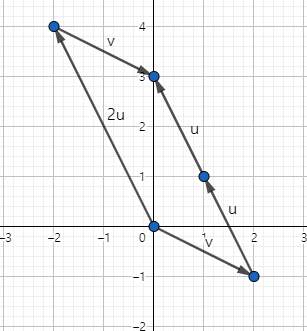
그러면 $u$가 두 배 늘어난 $2u$가 되게 됩니다. 이 상태에서 벡터의 덧셈을 풀어보겠습니다.

 

조금 더 편하게 보기 위해서 축 값들을 지웠습니다.

 

 

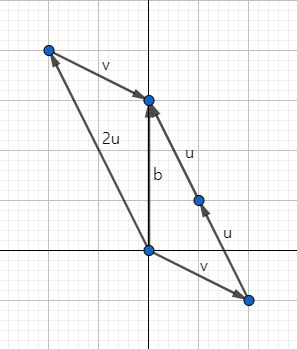
이렇게 방정식의 solution 벡터 $b$를 얻게 됩니다. 

 

 

 

column picture로 보는 것과 row picture로 보는 것은 무슨 차이가 있을까요?

 

3차원을 예로 들어보겠습니다.

$2x-y=0$

$-x+2y-z=-1$

$-3y+4z=4$

xyz 3차원 평면에 있습니다. 각 방정식을 만족하는 점을 전부 표현해 주겠습니다.

 

$A=\left[\begin{array}{ccccc}2& & -1& & 0\\ -1& & 2& & -1\\ 0& & -3& & 4\end{array}\right]b=\left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]$

 

 

 

- Row picture

 

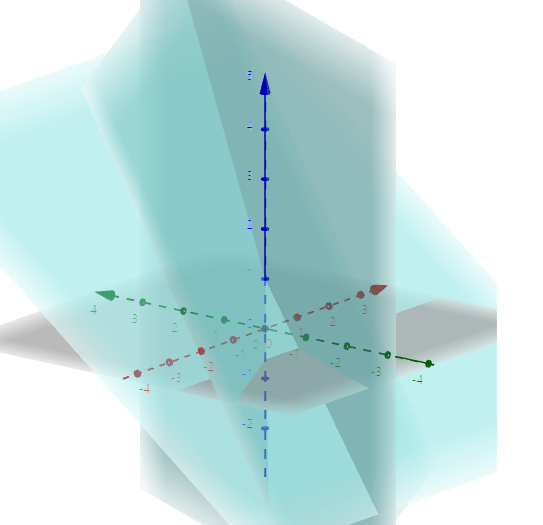
이제 방정식들을 모두 만족시키는 미지수를 찾아야합니다.

- 세 평면이 만나는 한 지점을 찾아야 됩니다.

- 하지만 차원이 올라갈수록 다음과 같이 점점 찾아보기가 어려워집니다.

- 시각화가 어려움

 

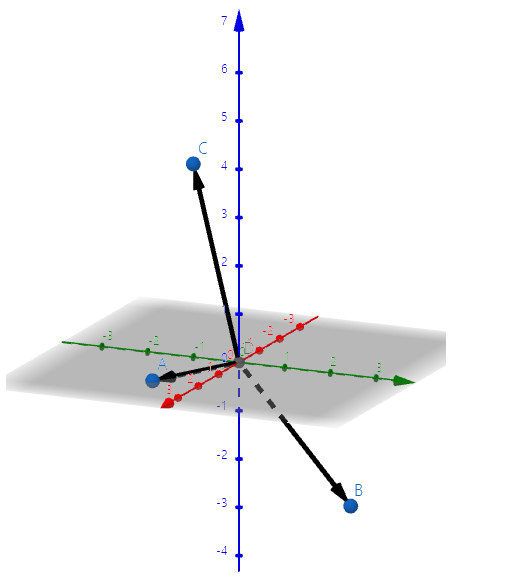
그럼 다시 column picture로 표현해봅시다.

 

 

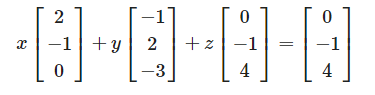
로 표현할 수 있습니다.

z = 1 만 나와주고 나머지가 0이 나오면 세 방정식을 만족시키는 미지수를 찾을 수 있습니다.

 

Row에서 봤다면 3개의 겹쳐진 평면에서 만나는 한 지점을 찾아야 했지만 Column에서 표현한다면 3가지 벡터로 조합되는 벡터를 찾으면 됩니다.

 

 

선형 연립 방정식 문제를 column으로 바라본다면 더 쉽게 solution을 찾을 수 있다가 이 강의의 핵심인 것 같습니다.

만약 row로 바라봤다면 3가지 평면이 겹쳐보이는 상황에서 한 지점을 찾아야하는 복잡한 문제였다면 여기서는 3가지 벡터를 더해서 얻어지는 벡터만 찾는 간단한 문제로 바뀐다는 것 같습니다. (시각화가 쉬움!)

 

 

물론 여기서는 column을 통해서 볼 수 없었던 것을 찾을 수 있었지만 항상 column으로 볼 수 있는 것은 아닙니다.

 

 

 

몇 가지 질문들

 

$Ax=b$에서 b값을 바꾼다면, b값이 바뀔 때 마다 $Ax$에는 b에 대한 모든 솔루션이 존재할까요?

- 다른 말로 바꿔 표현하자면 위에서 사용한 3가지 벡터로 $R^3$를 전부 표현할 수 있나요?

이 행렬은 선형독립이기 때문에 가능합니다.

 

 

 

 

 

요약

 

방정식 형태, 즉 row를 기준으로 문제를 바라볼 경우에는 방정식들을 만족시키는 모든 점들이 겹치는 부분을 찾아야 solution을 얻을 수 있지만 column을 기준으로 문제를 풀 경우 solution은 각 벡터들의 합으로 나오게 되어 비교적 간단하게 풀 수 있다. 또는 시각적으로 표현할 때 편하다.