방정식을 푸는 방법들은 다양합니다.
1. Elimination (소거법)
- Success
- Failure
2. Back-substitution (후방 대입법)
3. Elimination matrices (소거 행렬)
4. Matrix multiplication (행렬 곱)
여기서 소거법은 모든 소프트웨어 패키지가 방정식을 풀 때 사용하는 방법입니다.
- 소거법이 성공하면 solution을 얻습니다.
- 좋은 matrix에 대해서만 소거법을 진행했을 때 solution을 얻을 수 있습니다. (square matrix가 아닌 것도 solution을 얻을 수 있습니다.)
$ x + 2y + z = 2 $
$ 3x + 8y + z = 12 $
$ 4y + z = 2 $
다음과 같이 3개의 방정식과 3개의 미지수가 있습니다. 이전에 배운 방법을 사용해서 시스템 행렬 (system matirx)를 만들어 봅시다.
Success
$$ \left[\begin{matrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{matrix} \right] $$
2행 1열에 0을 얻었으니 다음은 3행 1열과 2열을 0으로 만들어야 합니다.
$$ \left[\begin{matrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 5 \end{matrix} \right] $$
이렇게 되면 3개의 피벗을 모두 찾았습니다. 작업이 완료된 행렬을 $u$라고 부르겠습니다. 소거법의 목표는 시스템 행렬 $A$를 $u$로 변경시켜주는 것입니다.
여기까지가 성공한 케이스고 이제 실패한 케이스에 대해서 알아보겠습니다.
Failure
위에 시스템 행렬은 1행, 1열의 숫자가 1이었습니다. 이 값이 0이었다면 피벗이 0이 되어 소거가 불가능합니다.
- 피벗 위치에 0이 존재한다면 행들을 교환해야 합니다. 행을 바꿔서도 피벗을 찾을 수 없다면 역행렬이 존재하지 않는 것입니다.
$$ \left[\begin{matrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & -4 \end{matrix} \right] $$
다음과 같은 경우에는 교체할만한 방정식이 없고 이 상태에서 소거법을 진행하면
$$ \left[\begin{matrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 0 \end{matrix} \right] $$
극복이 불가능한 complete failure가 돼버립니다.
- 이 경우 역행렬이 존재하지 않습니다. 위의 두 개의 방정식으로 마지막 방정식을 표현할 수 있어 소거를 진행하면 마지막 방정식이 전부 소거되기 때문입니다.
Back-substitution (역치환)
$Ax = b$에서 A만 사용해서 소거를 진행했지만 사실 b까지 고려해서 소거법을 사용해야 합니다. A와 b를 합쳐서 행렬을 만들어 보겠습니다.
$$ \left[\begin{matrix} 1 & 2 & 1 & 2 \\ 3 & 8 & 1 & 12 \\ 0 & 4 & 1 & 2 \end{matrix} \right] $$
column b를 추가로 가져왔습니다. 이것이 Augment matrix (증강행렬)이라고 합니다. 이 상태로 위에서 했던 소거법을 진행하면 됩니다.
- 여기서 b는 extra column이라고 합니다. 이렇게 소거를 진행하면 소거된 b를 얻을 수 있어서 미지수를 구할 수 있습니다.
후방 대입법을 이해하기 위해서 b까지 함께 고려한 소거법을 살펴보겠습니다.
$$ \left[\begin{matrix} 1 & 2 & 1 & 2 \\ 0 & 2 & -2 & 6 \\ 0 & 0 & 5 & -10 \end{matrix} \right] $$
$$ \left[\begin{matrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 5 \end{matrix} \right] = u$$
$$ \left[\begin{matrix} 2 \\ 6 \\ -10 \end{matrix} \right] = c$$
- 소거된 행렬 $A$는 $u$, 소거된 컬럼 벡터 $b$는 $c$로 표기합니다.
이것을 방정식으로 다시 정리하면($ux = c$)
$x + 2y + z = 2$ 여기서 $x = 2$
$2y - 2z = 6$ 여기서는 $y = 1$
$5z = -10$ $z = -2$ 라는 것을 알 수가 있습니다.
Elimination matrices (소거행렬)
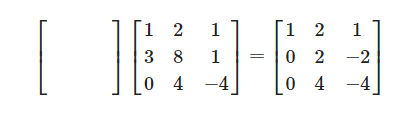
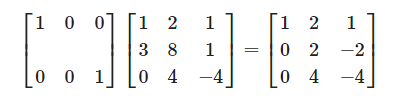
우리가 소거법을 사용하여 미지수의 값들을 찾았는데 이것을 행렬연산으로 표현해 보겠습니다. $EA =u$ 에서 $E$를 소거행렬이라고 합니다. ($A$행렬에 어떤 행렬을 곱해야 소거된 행렬이 나오는지 찾는 과정)
행렬 $A$의 1행을 그대로 가져오고 2행은 1열 원소를 제거된 상태로 만들어줍니다. 우선 2행 1열 성분을 제거하는 소거행렬이기 때문에 A의 3행도 변경없이 가져오면 됩니다.
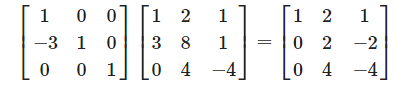
그러기 위해서는 행렬 $E$의 2행에서 1번째 원소를 -3을 주고 2번째 원소를 1을 주어서 3을 없애줍니다. 이 행렬을 $E_{21}$라고 부르겠습니다. (1행에 -3을 곱하고 2행과 더해주어 소거되는 과정)
이제 다음 단계 $E_{32}$를 구해봅시다. 위와 같은 방법으로 $A_{31}, A_{32}$성분을 소거해주기 위한 행렬을 만들어주면 됩니다.
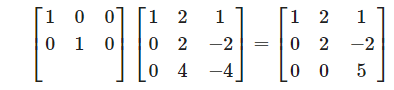
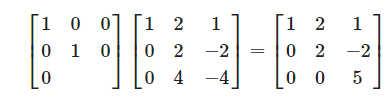
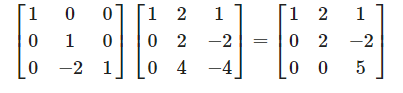
전체적인 과정을 살펴보면
- $E_{21}A$ 2행의 1열 원소를 소거해주고
- $E_{32}(E_{21}A) = u$ 3행의 1, 2열 원소를 소거해줍니다.
$(E_{32}E_{21})A = u$ 다음과 같이 행렬 E 두 개를 곱해주면 전체 과정을 한 번에 수행할 수 있는 행렬을 구할 수 있습니다. (선형적이어서 결합법칙이 성립한다.)
Permutation (치환행렬)
1행과 2행을 교환하는 과정을 행렬 연산으로 표현해보겠습니다.
다음과 같이 치환행렬 P와 A행렬이 존재할 때
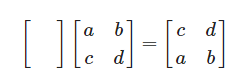
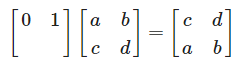
P의 1행에서 A행렬 2행만 가져오고
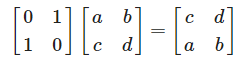
P의 2행에서 A행렬의 1행만 가져오면 됩니다.
$PA$가 아닌 $AP$는 어떻게 될까?
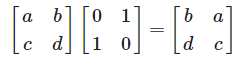
곱셈 순서를 바꿔주면 column을 변경할 수 있습니다.
- 어떤 순서로 곱하냐 따라서 행, 열이 바뀝니다. 즉 곱셈 순서에 따라서 연산의 의미가 바뀝니다. (교환법칙이 성립되지 않는다.)
Inverse matrix (역행렬)
소거를 통해서 A행렬을 u행렬로 바꿔줬는데 이제 다시 u행렬을 A행렬로 변경해보겠습니다.
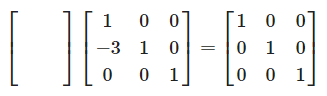
$E$ 행렬에 어떠한 행렬을 곱해서 항등행렬(indentity matrix)로 만들어줄 수 있다면 변환을 다시 되돌릴 수 있습니다. (이 어떠한 행렬을 $E^{-1}$이라고 하겠습니다.)
- $EA = u$
- $(E^{-1}E)A = E^{-1}u$
- $IA = A$
- 행렬 $E$ 1, 3 행은 유지하고 2행만 변경해주면 될 거 같습니다.
$E^{-1}$ 2행 부분을 $E$의 1행에 3을 곱하고 2행과 더해주게 만들어주면 됩니다.
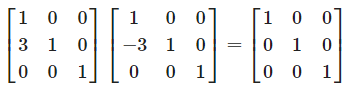
- 간단하게 생각하면 이전 연산에서 1행을 가져와서 3번 빼줬으니 그 역으로 3번 더해주면 되는 것입니다.
요약
- 연립일차방정식을 시스템 행렬로 만들고 나서 소거법을 사용하면 해를 구할 수 있다. 소거법을 통해서 소거가 완료된 행렬은 상삼각행렬이 된다. (피벗을 찾아주는 과정으로 인해서)
- 소거법은 연립해서 방정식을 푸는 과정을 행렬 연산으로 표현한 것인데 이때 소거행렬의 역행렬을 통해서 쉽게 원래 행렬을 찾을 수 있다.
- 치환행렬은 행을 교환하게 해주어 피벗을 찾는 과정을 도와줄 수 있고 곱하는 순서를 바꿔주게 되면 행이 아닌 열을 교환해준다.
- 소거된 행렬에서 원소가 모두 0인 행 벡터가 존재한다면 complete failure가 되고 선형종속을 의미하기 때문에 역행렬이 존재하지 않는다. (행을 교환해도 소거를 진행할 수 없어도 complete failure이다.)
- 소거법을 진행할 때 $Ax = b$에서 b벡터까지 고려해서 진행해야한다. (증강행렬로 만들어서 진행)
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 6. 열공간과 영공간(Column Space and Nullspace) (2) | 2022.01.27 |
|---|---|
| 5. 전치행렬, 치환행렬, 벡터 공간(Transposes, Permutations, Spaces R^n) (0) | 2022.01.26 |
| 4. LU decomposition (0) | 2022.01.22 |
| 3. 행렬곱셈과 역행렬(Matrix Multiplication and Inverse Matrices) (0) | 2022.01.21 |
| 1. Linear Algebra (0) | 2022.01.06 |