이전 두 강에서 행렬식과 행렬식의 속성에 대한 공식을 얻기 위해서 공부했습니다. 행렬식은 모든 정보를 단일 숫자로 묶습니다. 몇 차원 행렬이든지 행렬식의 결과값은 스칼라 값입니다. 이것이 역행렬과 어떤 관계가 있을까요?
$\left[\begin{matrix} a & b \\ c & d \end{matrix} \right]^{-1} = \frac 1 {ad - bc} \left[\begin{matrix} d & -b \\ -c & a \end{matrix} \right]$
$2 \times 2$ 행렬의 역에 대한 공식이 있습니다. 행렬식으로 교체된 행렬을 나눠주면 됩니다. 여기서 나눠지는 행렬의 1행 1열을 d를 보면 a의 cofactor라는 것을 알 수 있습니다.
-b는 c의 cofactor이듯이 이 행렬은 cofactor로 이루어진 행렬입니다. 여기서 왜 b는 -b가 됬을까요?
c의 cofactor인데 c의 위치를 보면 $c_{12}$로 i + j가 홀수가 나와서 음수가 된 것입니다.
정리하자면 어떤 행렬 A가 존재할 때 A의 역행렬은 A의 행렬식으로 전치된 여인수 행렬을 나눠주는 것으로 구할 수 있습니다.
$A^{-1} = \frac 1{det A} C^T$
이 식을 통해서 $AC^T =$ $ (det$ $A) I$도 성립하는지 알 수 있습니다. ($det$ $A$가 스칼라이기 때문에 matrix와의 덧셈에서는 identity matrix를 곱해줘야 합니다.)
- $A^{-1} = \frac 1 {detA}C^T$
- $(detA)A^{-1} = (detA)\frac 1 {det A} C^T$
- $(detA)A^{-1} = C^T$
- $A(detA)A^{-1} = AC^T$
- $(detA)AA^{-1} = AC^T$
- $(det)I = AC^T$
저번 시간에 얻은 det 공식을 다시 살펴보겠습니다.
$det$ $A = a_{i1}C_{i1} + a_{i2}C_{i2} + ... a_{in}C_{in}$
행렬 A와 C의 1행을 내적 한 것입니다. 이것을 계산해보게 된다면

다음과 같이 대각선 성분이 $det$ $A$인 행렬을 얻을 수 있습니다. 비대각선 성분들은 0으로 만들어 주어야 합니다.
내적을 할 때 비대각선 성분은 저절로 0이 되는데 그 이유는
$\left[\begin{matrix} a & b \\ c & d \end{matrix} \right]^{-1} = \frac 1 {ad - bc} \left[\begin{matrix} d & -b \\ -c & a \end{matrix} \right]$
다음 연산을 통해 만들어지는 행렬의 1행 2열 부분을 봐보겠습니다.
$AC^T = \left[\begin{matrix} a & b \\ c & d \end{matrix} \right]\left[\begin{matrix} d & -b \\ -c & a \end{matrix} \right]$
$\left[\begin{matrix} a & b \end{matrix} \right]_1 \left[\begin{matrix} -b \\ a \end{matrix} \right]_2 = -ab + ab$
이렇게 비대각 성분은 동일한 row에 대한 cofactor를 구하는 것이기 때문에 0이 나오게 됩니다.
Cramer's Rule
$Ax = b$ 문제에서 우리는 해당 조건을 만족하는 x를 찾기 위해서 $x = A^{-1}b$ 양변에 A의 역행렬을 곱해줄 수 있습니다. 이 역행렬은 위에서 배운 방법으로 $A^{-1} = \frac 1{det A}C^T$로 찾을 수 있습니다. Cramer's Rule은 여기서 x에 관한 식입니다.
여기서 $C^Tb$를 $B$라는 행렬로 바꿔서 진행해 보겠습니다. C는 A의 여인수들이 만들어낸 행렬이며 b와 내적을 진행하게 되는데 이것이 어떤 행렬 B의 행렬식을 구하는 형태가 됩니다. 이전에 $det$ $A$를 구할 때
$det$ $A = a_{i1}C_{i1} + a_{i2}C_{i2} + ... a_{in}C_{in}$
이런 형태였는데 여기서 $C^Tb$의 각 행들의 형태를 봐보면
$C^T_1b_1 = c_{11}b_1 + c_{12}b_2 + ... c_{1n}b_n$
위와 같은 형태가 됩니다. 그래서 이 식은 어떤 행렬 B의 행렬식(determinant)을 구하는 과정이라고 볼 수 있습니다.

$$x_1 = \frac {c_{11}b_1 + c_{12}b_2 + c_{13}b_3} {det A} = \frac {det B_1} {det A}$$
$$x_2 = \frac {c_{21}b_1 + c_{22}b_2 + c_{23}b_3} {det A} = \frac {det B_2} {det A}$$
$$x_2 = \frac {c_{31}b_1 + c_{32}b_2 + c_{33}b_3} {det A} = \frac {det B_3} {det A}$$
정리하자면 크래머 공식은 $Ax = b$를 만족시키는 x를 찾을 때 행렬식으로 유도된 공식을 통해 푸는 방법입니다. 이때 A는 정방행렬이면서 가역행렬이여야 합니다.
크래머 공식은 A의 행렬식을 구하고 B의 행렬식을 각각 구해야 하기 때문에 굉장히 비효율적인 방법입니다. 가우스 소거를 사용하는 방법이 더 효율적인 방법입니다.
행렬식은 무엇을 의미할까?
행렬식은 실제로 어떤 것의 부피와 같습니다. 3차원 공간 안에 존재하는 $3 \times 3$ 행렬에 대해서 이야기해보겠습니다. 행 벡터들이 다음과 같이 존재한다고 할 때

아래 사진과 같은 박스가 3차원 공간에 존재한다고 할 수 있습니다,.
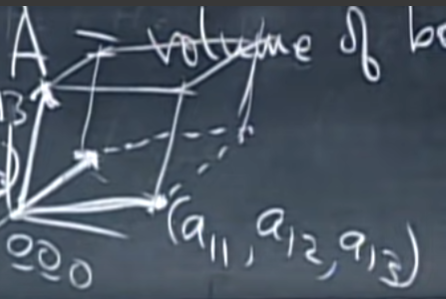
이 상자는 행렬식에 의해 부피가 주어진 상자입니다. 행렬식이 0이 된다면 상자의 밑변과 윗변이 같은 상황으로 입체적이지 않은 상태가 됩니다. (평면과 같은 형태로 부피가 0이 됩니다.)
행렬식을 사용해서 부피를 취하려면 절댓값을 취해야 합니다. 왜냐하면 행 교환이 일어나면 부호가 바뀌게 되는데 부피에는 마이너스가 존재하지 않기 때문입니다.
- 항등행렬의 부피는 1
다음으로는 직교행렬을 가져오겠습니다. $A = Q$ 이렇게 된다면 벡터들이 선형 종속되지 않아서 부피가 있는 상자를 만들 수 있을 것입니다.
$Q^TQ = I$
$det$ $Q^TQ = det$ $I$
$det$ $Q^2 = det$ $I$
행렬식의 특성 9번째와 10번째를 적용해 보겠습니다. 여기서 행렬식이 1이 나오게 되는데 이걸 위의 방법으로 해석해보면 3차원 공간에 존재하는 상자가 회전한 것으로 해석할 수 있습니다. 회전만 한 것으로 부피는 변하지 않는 것도 알 수 있습니다.
가장자리 벡터를 2배로 늘리게 되면 어떻게 될까요?
3번째 특성을 통해서 부피가 2배 늘어난 것을 알 수 있습니다.
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 22. Diagonalization and Powers of A (0) | 2022.05.15 |
|---|---|
| 21. Eigenvalues - Eigenvectors (0) | 2022.05.01 |
| 19. Determinant Formulas and Cofactors (0) | 2022.04.01 |
| 18. Properties of Determinants (0) | 2022.03.31 |
| 17. Orthogonal Matrices and Gram-Schmidt (0) | 2022.03.21 |