분류(Classification)는 data set(x, y)를 가지고 학습을 진행합니다. 그 이후 새로운 데이터 x'의 범주 y'을 예측하면 됩니다. 분류는 스팸메일, 게임 어뷰저, 신문기사 분류 등등에 사용됩니다. 특징으로는 Lable로 구분되는 값으로 값이 연속적이지 않습니다.
회귀(Regression)는 data set(x, y)를 가지고 x의 숫자 y를 예측하는 문제를 말합니다. 주가 예측, 경제 성장률 예측 등등에 활용되며 값이 연속적인 실수라는 특징이 있습니다.

Regression
위에서 말했듯이 회귀 문제는 주어진 데이터를 학습해 연속적인 예측값을 출력하는 모델입니다. 모델이란 해당 데이터들을 가장 잘 표현해줄 것 같은 가설(수학식으로 표현 되는 함수)로도 생각할 수 있습니다.
$H(x) = Wx + b$
다음과 같은 형태의 가설이 있다면 여기서 W는 기울기고 b는 편향을 의미합니다. 위 식은 우리의 모델을 행렬 방정식 형태로 기술한 것이고 다른 방법으로 표현한다면 $y = ax + b$ 다음과 같이 표현됩니다. 여기서 y는 영향을 받는 변수로 종속변수이고, x는 우리가 입력하는 값으로 영향을 주는 변수 독립변수입니다. 그리고 남은 a, b는 학습을 통해 찾아야 하는 최적값들입니다.
Regression vs Non-Regression
이제 선형 회귀와 비선형 회귀에 대해서 알아보겠습니다. 이 두 가지 모델 중 어떤 것을 사용하느냐는 우리가 접하는 데이터 분포에 따라서 달라집니다.

분석해야 되는 데이터의 분포가 일차식으로 표현 가능하다면 선형 함수를 그게 아니라면 비선형 함수를 사용하면 됩니다.
Cost function
비용함수(Cost function)은 모델을 어떤 방향으로 학습시킬지 결정하는 중요한 부분입니다. 여기서는 실제값과 예측값 사이의 오차를 통해서 판단하는 비용함수에 대해서 알아보겠습니다.
$Cost(W, b) = \frac 1 m \sum \limits_{i = 1}^{m} (H(x^{(i)}) - y^{(i)})^2$
$H(x)$ 예측값과 실제값의 차이를 제곱한 다음 평균을 내는 방법입니다. 출력된 값이 작을수록 예측을 잘 한 모델이 됩니다. cost = loss = object 전부 다 같은 함수를 지칭합니다.
Normal Equation
정규방정식은 선형 모델의 파라미터를 예측하기 위한 방법입니다. 비용함수가 최소가 되는 파라미터 벡터를 구하는 공식입니다.
$$\hat{w} = (X^TX)^{-1}X^Ty$$
비교적 모델의 특성이 적거나 샘플이 적은 단순한 경우에 사용하며 모델이 복잡해질수록 연산 시간이 크게 증가됩니다.
각 방정식들을 묶어서 행렬 방정식으로 만드는 것
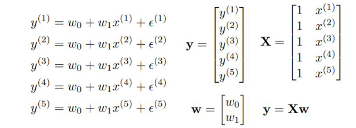
Optimizer
BGD(경사하강법): 경사하강법은 비용함수를 미분해 convex한 비용함수의 그래프의 접선 기울기가 0에 가까운 지점을 찾는 방법입니다. 비용이 최소가 되는 곳을 찾는 방법입니다.
- 모델의 비용함수값이 가장 낮아 모델이 잘 예측합니다.
$$cost(W, b) = \frac 1 m \sum \limits^m_{i = 1} (H(x^{(i)}) - y^{(i)})^2$$
$$W - \alpha \frac 1 m \sum (W(x_{i}) - y_{i})x_i$$
cost를 최소화시키는 W와 b를 구하는 것이 목적입니다. 현재 가중치가 적용된 cost function을 미분하여 새로운 가중치 값을 갱신합니다. 알파는 Learing rate로 매 step마다 정해진 기울기를 W에 얼만큼 반영하여 움직일지 정하는 하이퍼 파라미터입니다.

이 Learning rate를 잘 설정해줘야 하는데 너무 작을 경우 global minimum에 도달하는데 시간이 너무 오래 걸리며 너무 큰 경우 수렴하지 못하고 진동하게 됩니다. 그래서 요새는 adaptive learning rate라는 걸 사용해서 초기 Learning rate를 크게 잡고 학습이 진행함에 따라 점진적으로 감소하게 됩니다.
Regression 성능 평가
우리가 모델을 학습하고 나서 제대로 학습이 진행됐는지 확인해보기 위한 지표들이 존재합니다.
1. MAE(Mean Absolute Error)

실제값과 예측값의 차이 error를 절대값으로 변환해 평균화한 지표입니다. 일반적인 선형회귀의 성능지표입니다.
2. MSE(Mean Squared Error)

실제값과 예측값의 차이를 제곱해 평균화를 진행합니다. 예측값과 실제값 차이의 면적의 합으로 볼 수 있습니다. 선형회귀에서 자주 사용됩니다.
3. RMSE
$$RMSE(X,h) = \sqrt{\frac 1 m \sum \limits^m_{i = 1} (h(x^{(i)}) - y^{(i)})^2}$$
error 제곱의 sum에 루트를 씌운 형태
Multi Linear Regression and Polynomial Regression
Multi Linear Regression
다중선형회귀는 2차원 이상에서 정의된 데이터들을 잘 표현하는 평면이나 초평면을 찾는 것을 말합니다. (feature 특징들이 많다) 모델의 형태는 특징의 개수에 따라 직선, 평면, 4차원 이상의 공간 초평면이 됩니다. (독립변수가 많은 경우, 2개 이상인 경우)

Polynomial Regression
비선형 데이터를 학습하기 위해서 feature의 차수를 높인 형태 이 확장된 특성을 포함한 데이터셋에 선형모델을 훈련시킨 것을 말합니다. (다차원의 회귀식인 다항 회귀 분석은 단순한 선형 모델의 한계를 어느 정도 극복하게 할 수 있습니다. non linear 형태이기 때문에)

Binary Classification: 이진분류는 입력값에 따라 모델이 분류된 카테고리가 두 가지인 분류 알고리즘입니다.
Logistic Regression: 데이터가 어떤 범주에 속할 확률을 0~1 사이의 값으로 예측 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류합니다.
Sigmoid function: 0~1 사이에 커브 모양으로 만들어 주는 것으로 0~1 사이값 확률과 같은 형태로 출력값이 나옵니다.
Logistic loss function: $L = -(y \, log(a) + (1 - y)log(1 - a))$ a는 모델의 예측값이고 y는 타겟값
Softmax Regression: Logistic Regression에서 여러 개의 이진 분류기를 훈련시켜 연결하지 않고, 직접 다중 범주를 지원하도록 일반화한 것
Softmax funciton: $\frac {exp \, (s_k(x))} {\sum \limits^K_{j=i} exp \, (s_j(x))}$ 소프트맥스 회귀에 소프트맥스 함수를 적용하여 각 범주별 속할 확률을 추정합니다. (각 클래스에 속할 확률을 예측)
Cross Entropy: $L = - \frac 1 m \sum \limits^m_{i = 1} y_i \cdot log(\hat{y_i})$ 예측된 클래스의 확률이 실제로 얼마나 잘 맞는지 측정, 정답과 예측값의 차이를 계산
'BOAZ > 데이터 분석' 카테고리의 다른 글
| 3. Ensemble and Random Forest (0) | 2022.08.09 |
|---|---|
| 2. Decision Tree and SVM (0) | 2022.08.03 |
| [핸즈온 머신러닝] 3장 (0) | 2022.07.31 |
| [핸즈온 머신러닝] 2장 머신러닝 프로젝트 처음부터 끝까지 (0) | 2022.07.27 |
| [핸즈온 머신러닝] 1장 한눈에 보는 머신러닝 (0) | 2022.07.21 |