성능 측정
classification에 대한 평가를 진행할 때 사용하는 방법들에 대해 알아보겠습니다.
1. k-fold Cross Validation
분류를 진행하고 나서 성능 측정을 하는 방법 중에는 k-fold cross validation이 존재하는데 훈련 세트를 k개의 폴드로 나누고 각 폴드에 대해 예측을 만든 다음 평가하기 위해 나머지 폴드를 훈련시킨 모델에 사용하는 방법입니다.
2. Precision/Recall and Confusion Matrix
분류기의 성능을 평가하는데 오차 행렬(Confusion Matrix)로 각각의 분류 결과를 알 수 있습니다.

이런 오차 행렬의 정보를 요약한 지표가 존재하는데 그것이 정밀도(Precision)와 재현율(Recall)입니다.
정밀도는
정밀도와 재현율은 반비례합니다. 임계값이 높을수록 재현율은 낮아지고 정밀도는 높아집니다.

3. ROC 곡선
정밀도/재현율의 곡선과 유사하지만 ROC 곡선은 거짓 음성보다 거짓 양성이 중요하지 않을 때 사용하는 방법입니다.

Regression
Linear regression
선형회귀모형 예측: 이때,
비용함수는 다음과 같이 정의됩니다. MSE를 최소화하는
정규방정식: 비용함수를 최소화하는
정규방정식으로 학습된 선형 회귀 모델의 예측 속도는 빠르다는 장점이 있습니다.
예측 계산 복잡도는 샘플 수와 특성 수에 선형적입니다.

- 경사 하강법(Gradient Descent)
경사 하강법은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘입니다. 비용함수를 최소화하기 위해 반복해서 파라미터를 조정해나갑니다.
원리는 파라미터 벡터
경사 하강법의 하이퍼 파라미터로는 학습률(Learning rate)가 존재하는데 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행하므로 시간이 오래 걸리고 학습률이 너무 크다면 수렴하지 못하고 진동하게 됩니다. 그리고 경사 하강법을 진행하는 함수가 convex하지 않다면 local minumum에 수렴할 수 있습니다.
- 배치 경사 하강법(Batch Gradient Descent: BGD)
이를 비용함수의 기울기 벡터(gradient vector)라고 합니다.
이 방법은 매 스텝에서 훈련 데이터 전체를 사용하므로 매우 큰 훈련 세트에서는 학습 속도가 느립니다. 그러나 경사 하강법은 특성 수에 민감하지 않으므로 수십만 개의 특성에서 선형회귀를 훈련시키려면 경사 하강법을 사용하는 것이 빠릅니다.
- 확률적 경사 하강법(Stochastic Gradient Descent)
확률적 경사 하강법은 매 스텝에서 한 개의 무작위 샘플에 대한 그레디언트를 계산하여 진행됩니다. 그렇기 때문에 매 반복에서 다뤄야 할 데이터가 매우 적기 때문에 한 번에 하나의 샘플을 처리하면 알고리즘이 훨씬 빠릅니다. 그리고 비용함수가 convex하지 않을 때도 local minimum을 건너뛸 수 있도록 도와주므로 확률적 경사 하강법이 배치 경사 하강법보다 전역 최솟값을 찾을 가능성이 높습니다.
하지만 무작위 샘플 하나는 그 전체 데이터를 대표하지 못하며, 배치 경사 하강법보다 불안정합니다. 비용함수가 최솟값에 다다를 때까지 부드럽게 감소하지 않고 위아래로 요동치면서 감소하기 때문에 최솟값에 안착할 수 없습니다.
- 미니배치 경사 하강법(Mini-Batch Gradient Descent)
미니배치라 부르는 임의의 작은 샘플 세트에 대해 그레디언트를 계산합니다. 무작위 하나의 샘플을 고르는 것보다 데이터 대표성을 띌 수 있고 행렬 연산에 최적화된 하드웨어를 사용해서 성능이 향상되지만 지역 최솟값에서 빠져나오기 힘듭니다.
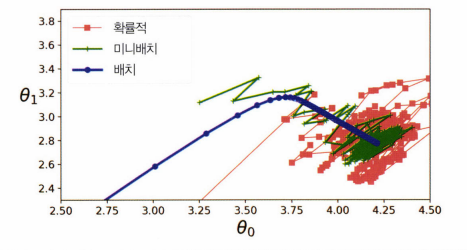
위 사진은 3가지 경사 하강법을 비교한 것입니다. 모두 최솟값 근처에 도달했습니다. 배치 경사 하강법은 실제로 최솟값에서 멈췄고 확률적 경사 하강법은 최솟값 근처를 맴돕니다.
Over fitting and Underfitting
- 과소적합(Under fitting)
두 곡선이 수평한 구간을 만들고 높은 오차에서 매우 근접해 있는 경우를 말합니다. (제대로 된 학습이 진행이 안됨)
비선형 데이터이므로 모델이 훈련 데이터를 완벽히 학습하는 것이 불가능합니다. 따라서 곡선이 어느정도 평평해질 때까지 오차가 계속해서 상승합니다. 선형 회귀의 직선은 데이터를 잘 모델링할 수 없으므로 오차 감소가 완만해집니다.

과소적합 해결법으로는 더 복잡한 모델을 사용하거나 더 나은 특성을 사용해야합니다.
과적합(Over fitting)
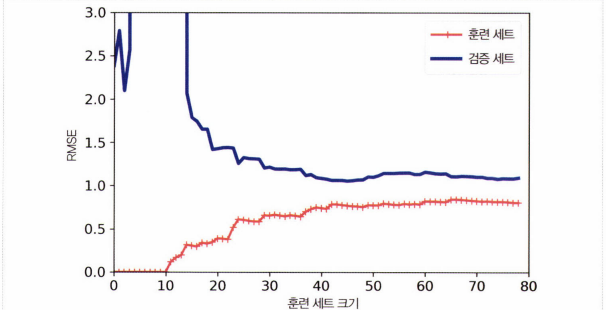
다음과 같이 validation set과 train set의 간격이 크게 존재하는 것을 알 수 있습니다. 이런 경우 과적합으로 볼 수 있습니다. 해결 방법으로는 검증 오차가 훈련 오차에 근접할 때까지 더 많은 훈련 데이터를 추가하거나 덜 복잡한 모델을 사용해야 합니다.
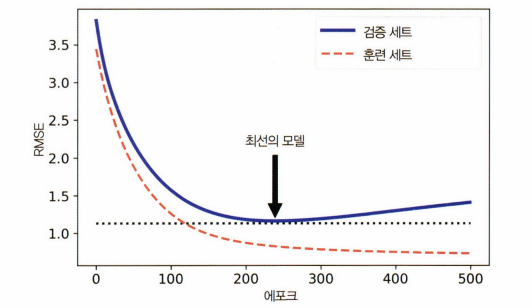
아니면 조기 종료를 사용하여 검증 에러가 최솟값에 도달할 때 훈련을 중지시키면 과적합이 되는 것을 막을 수 있습니다.
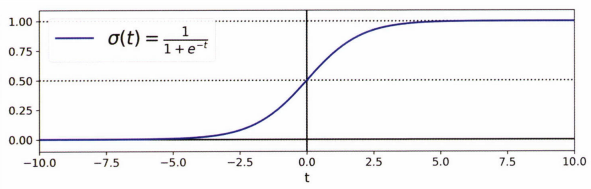
Logistic Regression
로지스틱 회귀 모델의 확률 추정은 다음과 같습니다.
이며
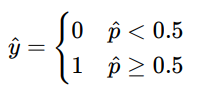
'BOAZ > 데이터 분석' 카테고리의 다른 글
| 3. Ensemble and Random Forest (0) | 2022.08.09 |
|---|---|
| 2. Decision Tree and SVM (0) | 2022.08.03 |
| 1. Classification and Regression (0) | 2022.07.28 |
| [핸즈온 머신러닝] 2장 머신러닝 프로젝트 처음부터 끝까지 (0) | 2022.07.27 |
| [핸즈온 머신러닝] 1장 한눈에 보는 머신러닝 (0) | 2022.07.21 |