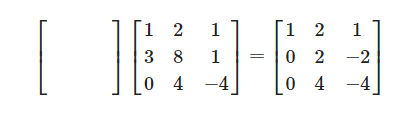ML, DL 정리 블로그

행렬 곱셈에 대한 규칙을 논의해보겠습니다. 1. Matrix multiplication 2. Inverse of $A$ $AB$ $A^T$ 3. Gauss - Jordan 행렬 곱셈에 대해 조금 더 알아보고 gauss - jordan을 사용하여 역행렬을 구하는 방법에 대해 알아보겠습니다. 행렬 곱셈에는 몇 가지 방법이 있는데 우선 $row \times column$에 대해 알아보겠습니다. 1. 행렬을 곱하는 방법 $row \times column$ 다음과 같은 행렬 연산이 있다고 해봅시다. ($AB = C$) $\left[\begin{matrix} & & & \\ & & & \\ a_{31} & a_{32} & a_{33} & a_{34} \end{matrix} \right] \left[\begin{ma..

방정식을 푸는 방법들은 다양합니다. 1. Elimination (소거법) - Success - Failure 2. Back-substitution (후방 대입법) 3. Elimination matrices (소거 행렬) 4. Matrix multiplication (행렬 곱) 여기서 소거법은 모든 소프트웨어 패키지가 방정식을 풀 때 사용하는 방법입니다. - 소거법이 성공하면 solution을 얻습니다. - 좋은 matrix에 대해서만 소거법을 진행했을 때 solution을 얻을 수 있습니다. (square matrix가 아닌 것도 solution을 얻을 수 있습니다.) $ x + 2y + z = 2 $ $ 3x + 8y + z = 12 $ $ 4y + z = 2 $ 다음과 같이 3개의 방정식과 3개의 미..

다음과 같이 두 개의 미지수를 가진 두 개의 방정식이 존재한다고 해봅시다. $2x - y = 0$ $-x + 2y = 3$ 이 두 방정식을 행렬로 표현한다면 각각의 계수와 미지수를 따로 묶어서 표현합니다. $$ \left[\begin{matrix} 2 & -1 \\ -1 & 2 \\ \end{matrix} \right] \left[\begin{matrix} x \\ y \\ \end{matrix} \right] = \left[\begin{matrix} 0 \\ 3 \\ \end{matrix} \right]$$ 방정식의 계수를 모아둔 행렬을 계수 행렬(coefficient matrix)이라고 부르고 $A$로 표기합니다. 그다음 미지수 벡터(the vector of unknown) 를 $x$ 마지막으로 이 ..