Integer Addition
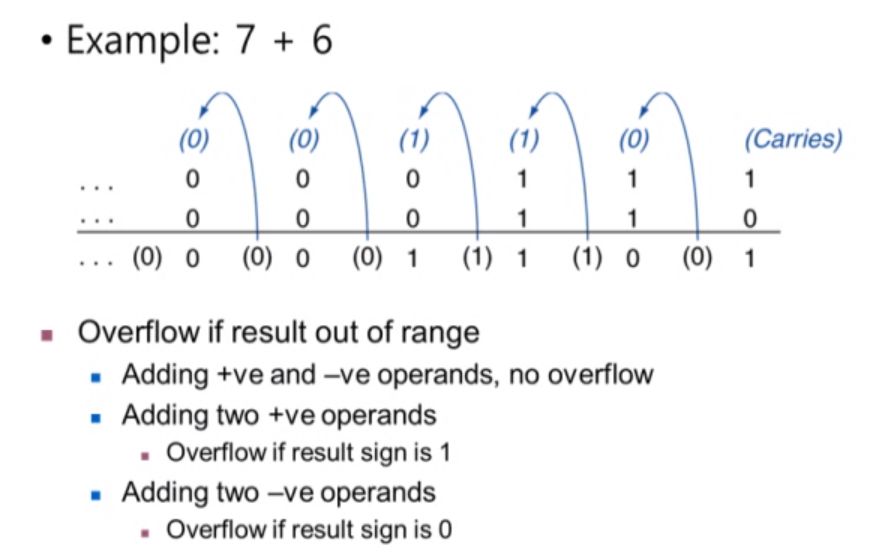
정수 덧셈 연산을 진행할 때 조심해야 할 것이 오버플로(overflow)입니다. 오버플로는 bit 범위를 벗어나는 경우를 말합니다. 양수와 음수를 더하는 경우에는 발생하지 않고 양수 두 개를 더해 sign bit이 1이 되거나 음수 두 개를 더했는데 sign이 0이 되는 경우에 발생하는 것입니다.

오버플로가 발생했을 때 프로그래밍 언어마다 처리하는 방식이 다릅니다. C언어의 경우 오버플로를 무시하기에 프로그래머들이 발생하지 않도록 해야 합니다.
Arithmetic for Multimedia

그래픽이나 음성을 처리하는 경우 8-bit, 16-bit 데이터를 많이 처리하게 됩니다. 64-bit adder를 사용하는 경우 8-bit를 8개, 16-bit을 4개 모아서 64 bit에 맞춰 연산을 처리할 수 있습니다. 이런 방식을 SIMD라고 부릅니다. SIMD를 사용하지 않는 경우 64-bit adder로 한 번에 한 개의 8-bit 데이터를 처리해야 합니다. Multimedia 연산 중 큰 특징이 saturating operation으로 오버플로가 발생하면 최대값으로 바꾸는 것입니다.
multiplication은 add 연산과 다르게 한 번에 진행되지 못하고 여러 번의 loop를 돌아야 합니다. 그래서 더하기 빼기 연산보다 더 많은 clock이 필요하게 됩니다.
Faster Multiplier

다음과 같이 많은 adder를 사용하여 여러 번 진행되는 덧셈 연산을 빠르게 할 수 있지만 비용이 증가하게 됩니다. 파이프 라인을 사용하는 경우 병렬적으로 처리하여 성능을 높일 수 있습니다.
Division

나누기 연산의 경우 우선 0인지 아닌지를 확인합니다. divisor가 dividend보다 작아야 하며 이 조건이 충족된다면 quotient bit을 0으로 하고 다음 bit로 내려가는 방식으로 동작합니다. 빼기를 했을 때 값이 음수가 된다면 다시 원래 값으로 돌려줘야 합니다.
곱셈의 경우 더하기만 했지만 나눗셈의 경우 값을 체크하고 뺏을 때 음수가 된다면 값을 다시 돌려주는 조금 더 복잡한 연산 과정을 거치게 됩니다. 부호가 있는 경우 나눗셈을 하면 절댓값으로 나누고 quotient와 remainder에 적절하게 sign값을 부여하면 됩니다.
Floating Point

이번에는 컴퓨터에서 어떻게 실수를 처리하는지 알아보겠습니다. 이 경우 정수형 수가 아닌 것들을 표현하는 방법으로 아주 작은 수와 큰 수를 표현할 수 있어야 합니다. normalized scientific notation은 소수점 위는 한 자리만 있게 표현하는 방식입니다. 0.002의 경우 1의 자리가 0이 아닌 수를 가져야 하기 때문에 nomalized 된 것이 아닙니다.

실수는 하드웨어를 만드는 회사마다 다르게 표현했기 때문에 표준화의 필요성이 있어, IEEE에서 표준을 만들었습니다. 이 표준에는 single precision과 double precision이 존재하는데 이것이 C언어의 float, double을 나타냅니다.

위 사진은 IEEE Floating Point Format으로 우선 제일 첫 번째 bit는 sign bit이고 exponent는 single이라면 8bits, double이라면 11 bits가 됩니다. fraction의 경우도 비슷하게 23 bits, 52 bits로 차이가 존재합니다. nomalized scientific notation의 소수점으로 표현되는 부분에서 1을 뺀 값을 fraction이라고 합니다. exponent는 지수값인 actualexponent에 bias 값을 더해서 저장합니다.

실수의 덧셈에 대해서 알아보겠습니다. 우선 decimal points를 맞추기 위해서 낮은 지수를 높은 지수에 맞춰줍니다. 그 이후 significands 두 개를 더합니다. 만약 일의 자리를 넘어섰다면 다시 nomalize를 진행해줍니다. 마지막으로 소수점 마지막 부분에서 반올림을 하여 자릿수를 맞춰줍니다. 가끔 9.9999 와 같은 값을 반올림하게 되면 10.000이 되기 때문에 renormalize를 할 필요가 생기게 됩니다.

FP의 Adder Hardware는 Integer Adder보다 더 복잡합니다. 한 사이클에 FP 덧셈을 진행하게 되면 clock cycle이 너무 길어지기 때문에 여러 사이클에 걸쳐 처리하게 됩니다. 이런 단점을 극복하기 위해서 파이프라인을 적용합니다.

FP multiplication은 지수를 먼저 더합니다. 그 이후 significands 끼리 곱하고 normalize를 진행합니다. 필요하다면 round와 renormalize를 적용합니다. 마지막으로 적절한 sign 값을 부여하면 됩니다.

이런 동작을 하는 FP multiplier는 significands를 곱하기 때문에 더 복잡한 하드웨어를 사용합니다. 사칙연산 외에 reciprcal과 square root 값을 제공해 주는 operation을 제공해 줍니다. 이런 operations은 여러 사이클이 걸리기에 파이프라인을 통해서 성능을 높여야 합니다.

FP hardware은 coprocessor로 제공이 되어 기존에 있는 프로세서에 FP hardware를 추가하는 방식입니다. 그래서 FP operation을 위한 레지스터가 별도로 존재합니다. FP instructions은 FP register에서만 동작합니다. 이를 통해 코드 사이즈가 늘어나는 것을 방지할 수 있습니다.

FP 연산에 대해서 rounding 할 때 여러 기법을 적용해볼 수 있습니다. precision을 정확히 하기 위해서 guard, round, sticky 사용합니다. 실수형 프로그램에서는 연산을 어떻게 조정하냐에 따라 정확도가 달라지기 때문에 위 기법들을 정밀하게 사용해야 합니다.
Parallelism
그래픽이나 오디오 같은 애플리케이션은 8, 16, 32 bit를 많이 사용하여 SIMD를 사용해 효율적으로 처리한다고 했습니다. SIMD 외에도 data level parallelism, vector parallelism 이라고도 부릅니다. (작은 연산들을 동시에 여러 개 한다고 하여 Subword Parallelism 이라고도 부릅니다.)
Right Shift and Division

signed / unsigned integer에서 bit를 옮길 때 i bit 만큼 left shift를 한 경우 2의 i승을 곱한 것과 같습니다. 반대로 right shift를 하는 경우에는 2의 i승으로 나눠주는 효과를 주는데 이건 unsigned integer에만 해당됩니다.
Associativity

병렬처리에서 계산 순서에 따라 값이 달라질 수 있습니다. 위 사진과 같은 변수들이 있을 때 x와 y를 먼저 더하고 z를 더하면 결과로 1.0이 나오지만 반대로 y와 z를 먼저 더하는 경우 y값이 z값보다 훨씬 커 제대로 값이 반영되지 않게 됩니다. 그래서 실수형 프로그램에서는 어떤 순서로 연산을 하는지가 굉장히 중요합니다. (Associativity가 중요)
규칙은 큰 수 끼리 먼저하고 나중에 작은 수를 처리하는 방식으로 진행하면 됩니다.

FP Accuracy는 scientific code에서 굉장히 중요합니다. 만약 계좌에서 하루에 0.0002센트씩 차이가 모든 사람들에게 적용된다면 굉장히 큰 금액의 손실이 생기게 됩니다.
Concluding Remarks

bits는 그 자체적으로 의미를 가지고 있지는 않습니다. 이 bits에 어떤 명령어를 적용함에 따라 bits가 명령어에 맞게 의미가 바뀔 수 있습니다.
컴퓨터는 숫자를 표현할 때 명확하게 표현할 수 없습니다. 다만 컴퓨터에서 사용하는 bits를 통해 가장 근사한 값으로 표현합니다. 그래서 실수형 프로그램을 사용할 때는 항상 finite range and precision을 잘 기억해야 합니다.
'CS > Computer Architecture' 카테고리의 다른 글
| 5. Instructions (0) | 2024.02.18 |
|---|---|
| 4. Instructions (0) | 2024.02.13 |
| 3. Instructions: Language of the Computer (1) | 2024.02.06 |
| 2. The Power wall (0) | 2024.02.06 |
| 1. Performance (2) | 2024.02.05 |