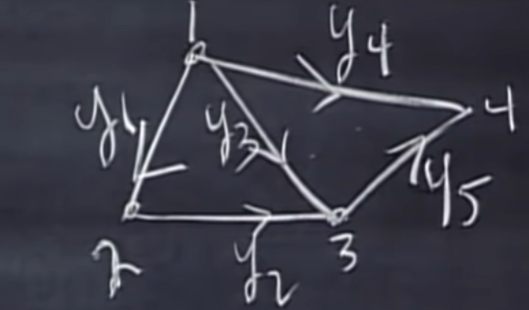
여기서 배우는 그래프는 객체들의 관계를 나타내는 구조를 말합니다.

위의 사진을 보면 그래프는 노드(node)와 엣지(edge)로 이루어져 있습니다. 방향을 가지는 엣지는 directed graph 방향이 없으면 undirected graph라고 합니다. 방향이 있는 경우 -, +를 표현할 수 있습니다.
- 노드는 사진에서 동그란 원 입니다.
그리고 그래프의 연결을 행렬로 표현할 수 있습니다. 위 사진을 표현하면 node = 4, edge = 5 이므로 $5 \times 4$ 형태의 행태인 행렬이 만들어집니다. edge가 column에 들어가는 방향인지 나오는 방향인지에 따라서 원소 부호가 정해지게 됩니다.
사진을 보면 노드들끼리 연결된 화살표들이 존재하는데 이런 연결 관계를 행렬로 표현할 수 있습니다. 연결 관계에 대한 행렬을 Incidence matrix라고 합니다.

루프는 총 3개가 있습니다.
- Loop1 : edge1, edge2, edge3
- Loop2 : edge3, edge4, edge5
- Loop3 : edge1, edge2, edge4, edge5
간단하게 생각하면 해당 그래프에서 만들어지는 도형의 개수만큼 루프가 만들어진다고 생각하면 됩니다. 지금은 삼각형 2개 평행사변형 1개가 만들어지니 총 3개의 루프가 나오게 됩니다.
여기서 엣지들이 모여 만든 삼각형들은 사각형안에 존재하고 있습니다. 두 삼각형 루프의 Incidence matrix는 사각형 루프 Incidence matrix의 subspace가 됩니다. 그리고 루프에 속하는 엣지들은 서로 선형종속입니다.

각 성분들은 엣지가 노드에 연결되어 있으면 1 그리고 들어가는 방향이면 + 나가는 방향이면 - 가 됩니다. 각 노드로 들어가고 나가는 엣지는 1개만 존재하므로 row 당 2개의 원소만 가질 수 있습니다. 그래서 크기가 커지면 희소 행렬이 됩니다.
- 희소 행렬 내부 구조를 분석하는 방법으로 null space를 찾는 방법이 있는데 이것을 통해 column에 해당하는 노드가 독립인지 아닌지 알 수 있습니다.
위에 행렬을 완성시킨 후 null space를 구해보겠습니다.
$Ax = \left[\begin{matrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{matrix} \right] \left[\begin{matrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{matrix} \right] = \left[\begin{matrix} x_2 - x_1 \\ x_3 - x_2 \\ x_3 - x_1 \\ x_4 - x_3 \end{matrix} \right] = \left[\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix} \right]$
조금 더 자세히 알아보기 위해서 전자 회로를 예시로 들어보겠습니다. 노드들을 전자 회로에서 전압을 측정하는 지점이라고 하고 $Ax = 0$에서 x벡터의 원소들을 각 노드에서의 전압이라고 한다면
- $Ax$을 통해 노드 간의 전위차를 계산할 수 있습니다.
- null space는 전위차가 모두 0인 경우입니다.
영벡터인 경우도 null space에 해당하지만 A의 각 column들을 보면 -1, 1이 하나씩만 존재해서 전부 다 더하면 0이 나온다는 것을 알 수 있습니다.
- 3개의 column은 독립이지만 마지막 column이 종속입니다.
$Ax = 0$
$x = c \left[\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix} \right]$
- dim N(A) = 1
node는 전압을 측정하는 장소이고 x는 전압이라고 했었습니다. ground는 어떤 의미를 가질까요?
node들 중 하나를 ground라고 설정하겠습니다. 그러면 이 node에서 측정되는 x는 0이 되게 됩니다.
마지막 노드를 ground로 설정해보겠습니다.
$Ax = x_1 \left[\begin{matrix} -1 \\ 0 \\ -1 \\ -1 \\ 0 \end{matrix} \right] + x_2 \left[\begin{matrix} 1 \\ -1 \\ 0 \\ 0 \\ 0 \end{matrix} \right] + x_3 \left[\begin{matrix} 0 \\ 1 \\ 1 \\ 0 \\ -1 \end{matrix} \right] + 0 \left[\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \\ 1 \end{matrix} \right]$
- 하나만 ground로 설정하는 이유는 Incidence matrix의 rank가 3이기 때문입니다.
Null space of $A^T$
이번에는 $A^T$의 null space를 구해보겠습니다. 이 부분은 키르히호프의 전류 법칙과 관련이 있습니다.
left null space는 $m \times n$의 경우 $m - rank$로 알 수 있기 때문에 $5-3 = 2$즉 $A^T$를 소거했을 때 free column이 2개가 나온다는 것을 알 수 있습니다. (left null space은 rank 2)
- rank의 경우 $A^T$와 A가 같습니다.
$A^Ty = \left[\begin{matrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{matrix} \right] \left[\begin{matrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{matrix} \right] = \left[\begin{matrix} -y_1 - y_3 - y_4 \\ y_1 - y_2 \\ y_2 + y_3 - y_5 \\ y_4 + y_5 \end{matrix} \right] = \left[\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix} \right]$
부호로 전류의 방향을 알 수 있습니다. node1에서는 edge1, edge3, edge4에서 다른 곳으로 전류가 나가는 것을 알 수 있습니다.
그리고 $ y_1 - y_2 = 0$을 보고 $y_1 = y_2$, $y_2 + y_3 = 5$을 통해서 node2, node3에서 들어오는 전류와 나가는 전류가 같은 것을 알 수 있습니다. (키르히호프의 전류 법칙)
left null space의 기저는
$\left[\begin{matrix} 1 \\ 1 \\ -1 \\ 0 \\ 0 \end{matrix} \right], \left[\begin{matrix} 0 \\ 0 \\ 1 \\ -1 \\ 1 \end{matrix} \right]$
left null space의 해는
$\left[\begin{matrix} 1 \\ 1 \\ 0 \\ -1 \\ 1 \end{matrix} \right]$이 나오게 됩니다.
- 이해하기 쉽게 해준다며 전자회로 내용으로 들어갔는데 오히려 이해하기가 더 힘들어진거 같습니다;;
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 14. Orthogonal vectors, subspace (0) | 2022.03.09 |
|---|---|
| 13. Quiz 1 Review (0) | 2022.03.02 |
| 11. Matrix Spaces: Rank 1: Small World Graphs (0) | 2022.02.17 |
| 10. The Four Fundamental Subspaces (0) | 2022.02.16 |
| 9. Independence, Basis and Dimension (0) | 2022.02.11 |