이번 강의는 $Ax = b$에 대한 복습을 해보겠습니다.
Q1. u, v, w가 $R^7$에 존재하며 0이 아닌 벡터일 때 이 벡터가 가지는 sapn의 rank는?
- 벡터가 3개 존재하니 최소 1차원, 최대 3차원입니다. (1 ~ 3차원)
Q2. $5 \times 3$ shape의 u행렬이 존재하며 피벗은 3개일 때 이 행렬의 null space는?
- 피벗이 3개이면 rank가 3이니 null space에 영벡터만 존재하게 됩니다. (1개)
Q3. $10 \times 3$ B행렬의 사다리꼴 형태는 무엇일까?

이 행렬을 echelon form(사다리꼴 행) 이라고 가정해보겠습니다.
$u, 2u$로 선형종속된 형태이니 소거를 진행해보면

한 가지 더 질문을 해보겠습니다. 이 행렬의 형태는 어떨까요? (Reduced row echelon form로 생각해 진행하겠습니다.)

이 행렬을 소거해보면 아래와 같습니다.

여기서 끝내지 않고 2행에 -1을 곱한 다음 소거를 계속해보겠습니다. (Reduced row echelon form이니)
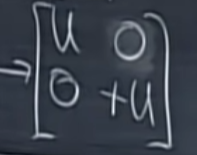
C 행렬의 rank는 몇 일까요? 오리지널 u행렬의 rank가 3이었으니 C는 rank가 6입니다.
- null space의 rank는 4입니다.
Q4. 행렬 A의 rank는?

- 우선 A는 3차원 벡터와 연산을 진행해 3차원 벡터가 나왔으니 $3 \times 3 matrix$입니다.
이 행렬의 null space 차원이 2가 되므로 A의 rank는 1이 됩니다.
$\left[\begin{matrix} 2 \\ 0 \\ 0 \end{matrix} \right], c \left[\begin{matrix} 1 \\ 1 \\ 0 \end{matrix} \right], d \left[\begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right]$ 에서 첫 번째 벡터는 particular solution이 되고 두 번째, 세 번째 벡터는 special solution이 됩니다. 이 모든 것을 다 합한 x는 complete solution이 됩니다.
그리고 행렬 연산을 역으로 생각해보면 A의 첫 번째 벡터에 $[2, 0, 0]^T$를 곱했을 때 $[2, 4, 2]^T$를 얻게되니 A의 첫 번째 column은 $[1, 2, 1]^T$가 되게 됩니다.
이후에 A의 rank는 1이기 때문에 나머지 column은 전부 선형종속된 형태입니다.
$A = \left[\begin{matrix} 1 & -1 & 0 \\ 2 & -2 & 0 \\ 1 & -1 & 0 \end{matrix} \right]$
짜투리로 나온 문제들
1. 행렬 A는 null space가 영벡터이고 square matrix이다.
- 이때 A의 전치행렬에 대한 null space 또한 영벡터이다.
2. 역행렬이 존재하는 $5 \times 5$ 행렬이 모든 $5 \times 5$ 행렬에 부분공간이 될 수 있을까?
- (zero matrix가 없기 때문에 불가능, 영벡터가 있어야 부분공간이 될 수 있다.)
3. 행렬 B에 대해서 $B^2 = 0$이면 $B = 0$ 인가?
$\left[\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix} \right]$
- 이 행렬을 제곱하면 zero matrix를 얻을 수 있다.
4. column들이 선형독립인 $n \times n$ 행렬이 존재할 때 $Ax = b$를 항상 풀 수 있나?
- column들이 독립적이라면 b는 항상 column들의 span에 존재합니다.
Q5. 행렬 B의 null space의 기저는?
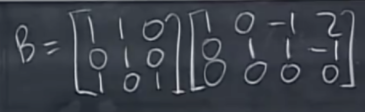
기저를 알기 위해서 $Bx = 0$을 풀어야 합니다. B는 (3 \times 3)(3 \times 4) = (3 \times 4) 형태 이므로 null space는 $R^4$에 존재합니다.
$N(CD) = N(D)$
$CDx = 0$
$C^{-1}CDx = C^{-1}0$
$Dx = 0$
즉 두 행렬의 곱셈 형태여도 C와 같이 역행렬이 존재한다면 굳이 연산을 안 하고 null space를 찾을 수 있다. (null space에 변화가 없으니)
이 행렬의 null space은 2개가 존재합니다.
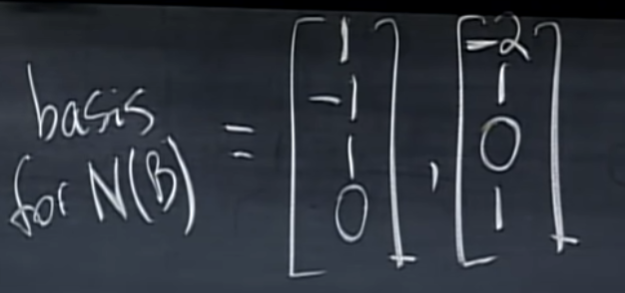
B의 $3 \times 4$ 행렬을 보면
$\left[\begin{matrix} I & F \\ 0 & 0 \end{matrix} \right]$ 형태인데 기저 벡터들도 1, 2 번째 row들을 보면 F이고 나머지 부분은 identity 인 것을 알 수 있습니다.
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 15. Projections onto Subspaces (0) | 2022.03.19 |
|---|---|
| 14. Orthogonal vectors, subspace (0) | 2022.03.09 |
| 12. Graphs, Networks, Incidence Matrices (0) | 2022.02.25 |
| 11. Matrix Spaces: Rank 1: Small World Graphs (0) | 2022.02.17 |
| 10. The Four Fundamental Subspaces (0) | 2022.02.16 |