$x_1y_1 +x_2y_2 = 0$
이번 강의에서는 orthogonality에 대한 강의입니다.
벡터, 부분공간, 기저가 직교한다는 것은 어떤 의미일까요?
10강에서 사용했던 이미지를 다시 한번 봐보겠습니다.

이 이미지에서는 많은 정보를 얻을 수 있습니다. 각 space의 차원과 차원들이 이루는 각도에 대한 정보를 가지고 있는데 여기서 필요한 정보는 부분공간 사이의 각도가 90도가 된다는 것입니다.
null space와 row space의 관게를 나타낼 때 사용하던 것이 $Ax = 0$ 이었습니다. 여기서 알 수 있듯이 직교성을 테스트하는 방법으로 내적을 활용한다는 것을 알 수 있습니다.
이제 벡터로 넘어가 보겠습니다.

다음과 같이 orthogonal한 x벡터와 y벡터가 존재할 때 n차원 공간에서 벡터 사이의 각도가 90도임을 의미합니다.
이러한 벡터의 직교성을 테스트하는 방법도 위에 부분공간의 직교성을 확인한 것과 같이 내적을 이용하는 것입니다.
$x^Ty = 0$
조금 더 풀어서 봐보면
$x_1y_1 +x_2y_2 = 0$
$||x||^2 + ||y||^2 = ||x+y||^2$
- 직각 삼각형에서 알 수 있듯이 x벡터의 길이 제곱과 y벡터 길이 제곱을 더하면 x+y 길이 제곱과 같을 경우
이 내적의 결과가 0이 된다면 이 벡터들이 orthogonal 하다는 것을 알 수 있습니다.
예시를 하나 들어보겠습니다.

각각 길이의 제곱을 구한 뒤 비교해보니 14 + 5로 19와 일치한다는 것을 알 수 있었습니다. 조금 더 간단하게 해보자면
$||x||^2 + ||y||^2 = ||x+y||^2$
$x^Tx + y^Ty = (x + y)^T(x+y)$
$= x^Tx + y^Ty + x^Ty + y^Tx$
- $ x^Ty = y^Tx$ 이니
$x^Tx + y^Ty = x^Tx + y^Ty + x^Ty + y^Tx$
$x^Tx + y^Ty = x^Tx + y^Ty + 2x^Ty$
양변에 각각 벡터의 길이 제곱을 빼주면
$0 = 2x^Ty$
$x^Ty = 0$ 이것을 통해서 직교하는 벡터의 내적도 0이 된다는 것을 알 수 있습니다.
subspace
다음으로 부분공간이 직교한다는 것을 알아보겠습니다.
두 부분공간 S와 T가 직교한다라고 했을 때 무엇을 의미할까요?
- S의 모든 벡터와 T의 모든 벡터들이 직교를 이룬다.
우리가 배운 부분공간 중 직교하는 공간은 대표적으로 row space와 null space가 있습니다.
$Ax = 0$ 이때 A의 행과 x가 직교를 해서 0이 나오는 것입니다.
하지만 이것들은 A의 일부분 벡터들로 row space 전체와 x가 수직이라고 말할 수는 없습니다.
$c_1(row_1)^Tx = 0$
$c_2(row_2)^Tx = 0$
$(c_1row_1c_2row_2)^Tx = 0$
다음과 같이 각 row들에 상수배를 하여 선형 조합들의 직교도 확인할 수 있습니다.
- row space와 null space의 모든 벡터들은 직교해야 한다.
- column space와 left null space의 모든 벡터도 직교해야 합니다.
우리가 누군가의 맥박 수를 측정한다고 해봅시다. 측정값에는 많은 노이즈가 존재할 것입니다. 이렇게 많은 문제들에서 우리는 많은 방정식을 가지고 있고 거기에 노이즈가 존재하기 때문에
$Ax = b$ 정확하게 풀기 어렵습니다. (solution이 없을 때도 항상 풀 수 있게)
행렬이 방정식이 더 많을 때 이것은 미지수의 개수보다 더 많을 텐데 우리는 모든 측정값을 사용하길 원하고, 그래서 최적의 솔루션을 찾기를 원합니다. (A가 직사각형)
이러한 솔루션을 찾는 방법으로 $A^TA$같은 좋은 형태를 가진 행렬을 사용하면 best solution을 찾을 수 있습니다.
- 이러한 행렬의 특징은 square matrix이고 symmetric matrix이다.
$(A^TA)^T = A^TA$
이 행렬을 사용해서 $Ax = b$를 푸는 방법으로는
$A^TAx = A^Tb$ 양변에 $A^T$를 곱해주는 것입니다.
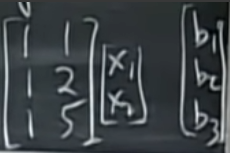
A가 다음과 같이 ractangular matrix일 때

$A^TA$를 해주면 다음과 같이 역행렬을 찾을 수 있는 대칭행렬이 나오게 됩니다.
하지만 항상 이렇게 가역행렬이 나오는 것은 아닙니다.
- 역행렬이 존재하니 양변에 역행렬을 곱해주면 b에 대한 솔루션 x를 찾을 수 있음
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 16. Projection Matrices and Least Squares (0) | 2022.03.20 |
|---|---|
| 15. Projections onto Subspaces (0) | 2022.03.19 |
| 13. Quiz 1 Review (0) | 2022.03.02 |
| 12. Graphs, Networks, Incidence Matrices (0) | 2022.02.25 |
| 11. Matrix Spaces: Rank 1: Small World Graphs (0) | 2022.02.17 |