이번 강의는 굉장히 중요한 내용입니다.
투영에 관한 강의인데 바로 b벡터를 a벡터에 투영해보겠습니다.

다음과 같이 다른 선상에 존재하는 두 벡터가 존재할 때 투영하는 방법에 대해서 알아보겠습니다. 우선 a선상에서 b벡터와 가장 가까운 점을 찾습니다. (이 점을 P라고 부릅니다.)

그리고 그 점과 b벡터를 연결하면 b에서 내려진 수선의 발과 a가 이루는 각도는 직교가 됩니다.

수선의 발을 e라고 했을 때 $e = b - p$가 됩니다. 벡터 p는 a벡터에 스칼라곱을 한 형태입니다.
- $p = xa$ x는 임의의 상수
모든 핵심은 수선의 발 e와 a벡터가 이루는 각도가 수직이라는 것입니다.
$a^T(b - xa) = 0$
$a^T(e) = 0$
- a와 e는 수직입니다.
우선 첫 번째 방정식을 풀어주겠습니다.
$a^T(b - xa) = 0$
$a^Tb - xa^Ta = 0$
$xa^Ta = a^Tb$
$x = \frac {a^Tb} {a^Ta}$
분모, 분자가 내적으로 만들어진 것이니 결과값도 상수값입니다.
$p = xa$이니
$p = a \frac {a^Tb}{a^Ta}$
$p = \frac {aa^T}{a^Ta}b$
만약 b벡터를 두 배로 늘리면 어떻게 될까요? p벡터도 두 배로 늘어나게 됩니다.
- 투영이 두 배로 멀리 감
a를 두 배로 늘리면 어떻게 될까요?
- 투영은 그대로 있습니다.
즉 b에 어떠한 변환을 시켜 벡터 a로 이동하는 것인데 이때의 변환을 투영행렬과의 곱으로 표현합니다.
$P = \frac {aa^T}{a^Ta}$, 투영을 시켜주는 매개체
$p = Pb$, 투영된 벡터
$\left[\begin{matrix} 2 & 4 \\ 3 & 5 \end{matrix} \right]^A \left[\begin{matrix} 2 \\ 6 \end{matrix} \right] = 2 \left[\begin{matrix} 2 \\ 3 \end{matrix} \right] + 6 \left[\begin{matrix} 3 \\ 5 \end{matrix} \right] = \left[\begin{matrix} 22 \\ 36 \end{matrix} \right]$
행렬과 벡터를 곱하면 다음과 같이 벡터의 원소들이 행렬의 column에 곱해져서 더해지는 즉 column vector의 선형조합으로 표현되게 됩니다.
- 행렬에 벡터를 곱하면 그 행렬의 column space에 들어가게 된다, 투영행렬에 벡터를 곱하면 a벡터가 지나가는 선상으로 벡터가 들어가게 된다.
- 벡터 b를 두 번 투영시키면 어떻게 될까? 이 경우에는 첫 번째와 변함이 없다.
$P^2 = P$로 표현이 된다.
- 투영행렬은 $aa^T$ 처럼 column vector $\times$ row vector이므로 대칭행렬이며 rank가 1인 행렬이다.
왜 투영(projection)을 할까요?
$Ax = b$에 대한 솔루션이 없을 때, b가 A의 span에 존재하지 않을 경우 근사한 값을 찾기 위해서입니다.
- b와 A의 span에서 가장 가까운 점을 찾고 수선의 발을 내려 근사하는 것!
아래 사진과 같이 $Ax = p$로 푸는 것입니다.

여기서 p는 평면에 존재하는 벡터 $a_1, a_2$의 선형조합으로 표현할 수 있습니다.
$p = x_1a_1 + x_2a_2$
이렇게 근사를 했을 때 우리의 목표는 근사된 값과 실제 값 b의 오류를 최대한 줄이는 것입니다.
오류를 e라고 표현했을 때
오류 벡터 e와 투영을 원하는 공간이 수직이라면 오류 값이 최소가 됩니다.
- 가장 가까운 거리에 존재하는 경우
- $Ax = b$, $x$는 실제값 $b$를 찾아주는 벡터이고 $\hat{x}$은 투영된 값 $p$를 찾아주는 벡터!
$A \hat{x} = p$
$A^T(b - A \hat{x}) = 0$
$A^T(b - p) = 0$
$A^Te = 0$
- 투영 공간에 존재하는 행렬과 내적 해서 0이 된다면 수직! (가장 오차가 적은 부분!)
- 이렇게 구한 e는 $A^Te = 0$를 만족시키니 $A^T$의 null space에 존재합니다.
정리해보자면, 투영된 p를 찾아주는 벡터 $\hat {x}$는
$A^TA \hat{x} = A^Tb$
$\hat{x} = (A^TA)^{-1}A^Tb$
$p = A \hat{x} = A(A^TA)^{-1}A^Tb$, (투영된 값)
$P = A(A^TA)^{-1}A^T$, (투영행렬)
식을 조금 전개하면 정리를 더할 수 있을 거 같으니 전개를 해보자!
$P = A(A^TA)^{-1}A^T = AA{-1}(A^T)^{-1}A^T = I$
단위행렬이 나오게 되는데 이 매번 그런 것이 아니라 행렬 A가 square matrix이고 가역행렬일 때만 가능한 것입니다.
대부분의 문제 같이 방정식이 미지수보다 많은 rectangular matrix인 경우에는 성립되지 않습니다.
$P^T = P, P^2$ 조건에도 만족하는지 알아보겠습니다.
- $P^T = (A(A^TA)^{-1}A^T)^T = A^{TT}(A^TA^{TT})^{-1}A^T = A(A^TA)^{-1}A^T$
- $P^2 = A(A^TA)^{-1} [A^TA(A^TA)^{-1}] A^T = A(A^TA)^{-1}A^T$
- 1번의 경우 $(A^T)^{-1} = (A^{-1})^T$
예시
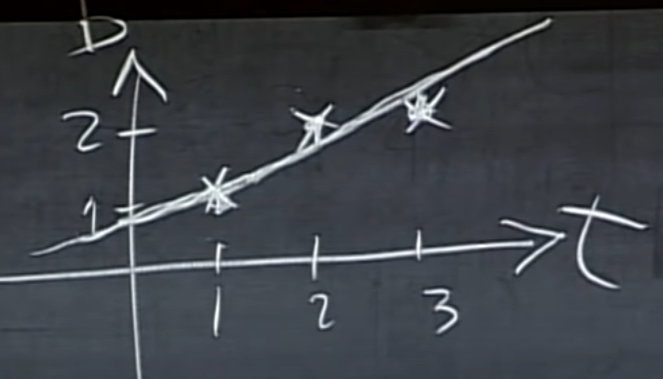
다음과 같이 우리의 직선상에 데이터가 존재하지 않을 때 직선과 데이터 간의 거리가 error가 됩니다.
우리 직선의 가설은 $b = C + Dt$입니다.
- 데이터는 (1, 1), (2, 2), (3, 2)입니다.
우리는 직선이 최대한 3개의 데이터와 가깝게 지나가는 것을 원하기 때문에 적절한 C와 D값을 찾아야 합니다.
이제 데이터의 t값과 b값을 대입해보면
$C + D =1$
$C + 2D =2$
$C + 3D =2$
이렇게 3개의 방정식을 얻을 수 있습니다. 행렬로 표현해보겠습니다.
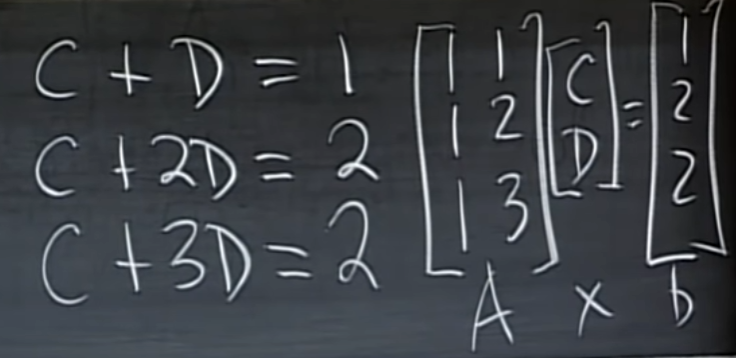
$Ax = b$와 같은 식을 얻었는데 b가 A의 span에 존재하지 않는다면 우리가 위에서 구한 식으로 간단하게 풀 수 있습니다.
- $A^TA \hat{x} = A^Tb$ 양변에 $A^T$만 곱하여 문제를 해결!
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 17. Orthogonal Matrices and Gram-Schmidt (0) | 2022.03.21 |
|---|---|
| 16. Projection Matrices and Least Squares (0) | 2022.03.20 |
| 14. Orthogonal vectors, subspace (0) | 2022.03.09 |
| 13. Quiz 1 Review (0) | 2022.03.02 |
| 12. Graphs, Networks, Incidence Matrices (0) | 2022.02.25 |