이번 강의는 굉장히 중요한 내용입니다.
투영에 관한 강의인데 바로 b벡터를 a벡터에 투영해보겠습니다.

다음과 같이 다른 선상에 존재하는 두 벡터가 존재할 때 투영하는 방법에 대해서 알아보겠습니다. 우선 a선상에서 b벡터와 가장 가까운 점을 찾습니다. (이 점을 P라고 부릅니다.)

그리고 그 점과 b벡터를 연결하면 b에서 내려진 수선의 발과 a가 이루는 각도는 직교가 됩니다.

수선의 발을 e라고 했을 때
-
모든 핵심은 수선의 발 e와 a벡터가 이루는 각도가 수직이라는 것입니다.
- a와 e는 수직입니다.
우선 첫 번째 방정식을 풀어주겠습니다.
분모, 분자가 내적으로 만들어진 것이니 결과값도 상수값입니다.
만약 b벡터를 두 배로 늘리면 어떻게 될까요? p벡터도 두 배로 늘어나게 됩니다.
- 투영이 두 배로 멀리 감
a를 두 배로 늘리면 어떻게 될까요?
- 투영은 그대로 있습니다.
즉 b에 어떠한 변환을 시켜 벡터 a로 이동하는 것인데 이때의 변환을 투영행렬과의 곱으로 표현합니다.
행렬과 벡터를 곱하면 다음과 같이 벡터의 원소들이 행렬의 column에 곱해져서 더해지는 즉 column vector의 선형조합으로 표현되게 됩니다.
- 행렬에 벡터를 곱하면 그 행렬의 column space에 들어가게 된다, 투영행렬에 벡터를 곱하면 a벡터가 지나가는 선상으로 벡터가 들어가게 된다.
- 벡터 b를 두 번 투영시키면 어떻게 될까? 이 경우에는 첫 번째와 변함이 없다.
- 투영행렬은
왜 투영(projection)을 할까요?
- b와 A의 span에서 가장 가까운 점을 찾고 수선의 발을 내려 근사하는 것!
아래 사진과 같이

여기서 p는 평면에 존재하는 벡터
이렇게 근사를 했을 때 우리의 목표는 근사된 값과 실제 값 b의 오류를 최대한 줄이는 것입니다.
오류를 e라고 표현했을 때
오류 벡터 e와 투영을 원하는 공간이 수직이라면 오류 값이 최소가 됩니다.
- 가장 가까운 거리에 존재하는 경우
- 투영 공간에 존재하는 행렬과 내적 해서 0이 된다면 수직! (가장 오차가 적은 부분!)
- 이렇게 구한 e는
정리해보자면, 투영된 p를 찾아주는 벡터
식을 조금 전개하면 정리를 더할 수 있을 거 같으니 전개를 해보자!
단위행렬이 나오게 되는데 이 매번 그런 것이 아니라 행렬 A가 square matrix이고 가역행렬일 때만 가능한 것입니다.
대부분의 문제 같이 방정식이 미지수보다 많은 rectangular matrix인 경우에는 성립되지 않습니다.
- 1번의 경우
예시
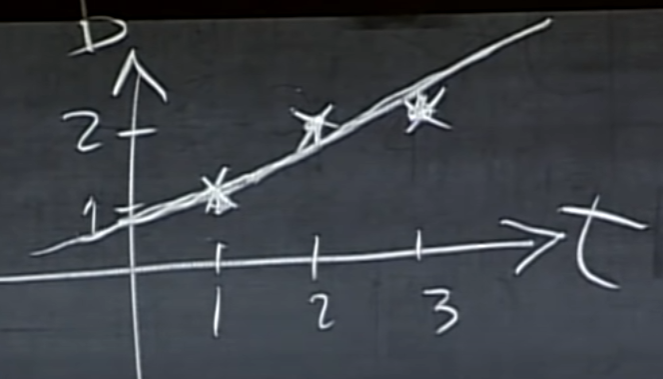
다음과 같이 우리의 직선상에 데이터가 존재하지 않을 때 직선과 데이터 간의 거리가 error가 됩니다.
우리 직선의 가설은
- 데이터는 (1, 1), (2, 2), (3, 2)입니다.
우리는 직선이 최대한 3개의 데이터와 가깝게 지나가는 것을 원하기 때문에 적절한 C와 D값을 찾아야 합니다.
이제 데이터의 t값과 b값을 대입해보면
이렇게 3개의 방정식을 얻을 수 있습니다. 행렬로 표현해보겠습니다.
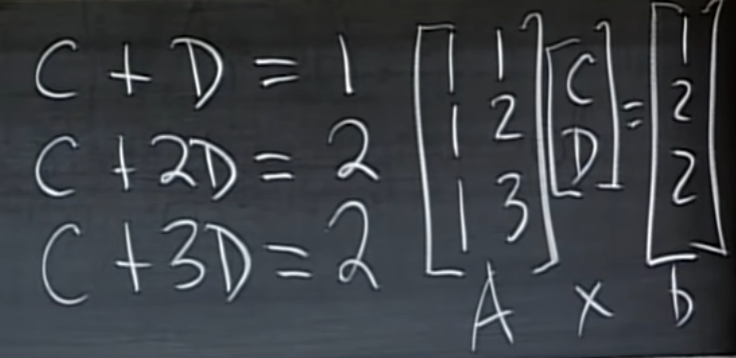
-
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 17. Orthogonal Matrices and Gram-Schmidt (0) | 2022.03.21 |
|---|---|
| 16. Projection Matrices and Least Squares (0) | 2022.03.20 |
| 14. Orthogonal vectors, subspace (0) | 2022.03.09 |
| 13. Quiz 1 Review (0) | 2022.03.02 |
| 12. Graphs, Networks, Incidence Matrices (0) | 2022.02.25 |