ML, DL 정리 블로그

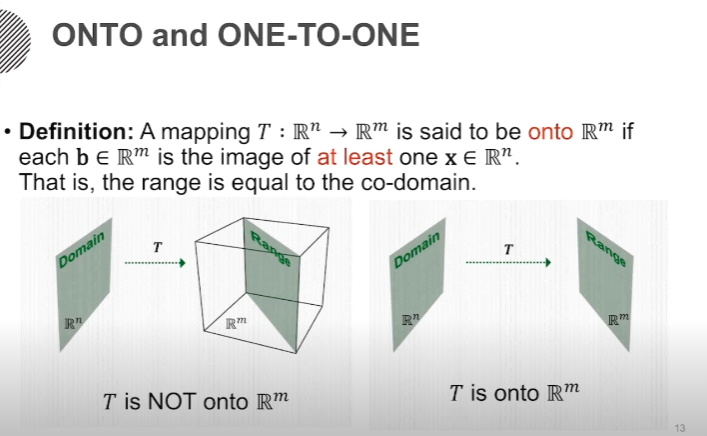
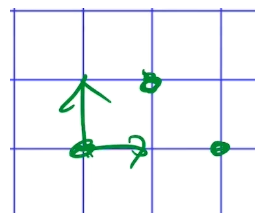
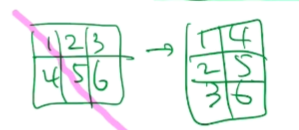
- 본 내용은 edwith의 인공지능을 위한 선형대수 강의를 통해 작성되었습니다. 이번 학습의 목표는 Least Squares Ploblem에 대한 개념을 이해하는 것 입입니다. 벡터와 관련된 이 개념들은 선형대수에서 중요한 개념이니 알아두면 좋습니다. 핵심 키워드 내적(Inner Product, Dot Product) 벡터의 길이(Vector Norm) 단위벡터(Unit Vector) 직교벡터(Orthogonal Vectors) Leaset Squares = 선형 방정식을 다루는 상황에서 방정식의 개수가 미지수의 개수보다 많은 상황일 때를 말합니다. - feature의 개수보다 데이터 개수가 더 많을 때 방정식이 3개이고 미지수가 3개인 이 상태에서 데이터를 더 수집한다면 방정식의 개수가 늘어나게 됩니..

전사함수와 일대일 함수 (ONTO and ONE - TO - ONE) ONTO ONTO는 공역(입력) = 치역(출력이 될 수 있는 애들)일 때 이 경우를 ONTO라고 부릅니다. 공역과 치역이 같을 때! 공역과 치역이 같을 때 필요한 최소한의 조건은 정의역이 치역 이상이어야 합니다. 즉 치역의 모든 원소를 한번 이상의 매핑이 필요합니다. 1. $R^3 \rightarrow R^2$ 2. $R^2 \rightarrow R^3$ 2번째의 경우에는 절대 전사함수가 될 수 없습니다. 위에서 말한 최소한의 조건을 만족시키지 못했기 때문입니다. - 입력 Dimention이 출력 Dimention보다 작으면 안 됩니다. $T ( \left [ \begin{matrix} 1 \\ 0 \end{matrix} \right]..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. 선형변환은 신경망에서 가장 기초적인 형태입니다. 선형변환에서 일어나는 일은 결과에 따라 Standard vector값이 바뀌면서 좌표도 바뀌게 됩니다. $[1, 0], [0, 1]$이였던 벡터가 선형변환을 통해서 $[2, 3]$과 같은 형태로 바뀌고 그에 따라 좌표도 변경된 것입니다. - 선형변환을 기하학적으로 표현한 것! 이 사진에서는 56, 231, 24, 2 값을 가지는 이미지가 벡터화가 돼서 입력층으로 들어갑니다. 이 구조가 이전 게시물에서 말했던 fully connected layer의 모습입니다. 옆에 $(3 \times 4)$ 행렬과 $(4 \times 1)$ 벡터가 있는데 여기서 행렬은 3차원으로 shape..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. 함수의 입력으로 쓰이는 모든 집합은 정의역(domain), 함수의 출력값으로 쓰이는 모든 output의 집합은 공역(co-domain), 입력에 대한 출력값은 image라고 합니다. range는 치역으로 실제로 사용된 공역입니다. ex) $2x$라는 함수가 있을 때 $x = 1$의 image는 2 선형변환의 조건 $T(cu + dv) = cT(u) + dT(v)$을 만족할 때 ($u, v$는 벡터입니다.) $3x$와 같은 단순 상수배이면 선형변환이 됩니다. $y = 3x + 2$와 같이 bias가 포함되면 선형변환이 아닙니다. 위 조건을 만족시키지 않기 때문입니다. 하지만 이러한 경우도 수정을 해주면 선형변환이라고 할 수..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. subspace는 부분공간, 부분집합으로 생각하시면 됩니다. span과 유사한 개념입니다. $R^3$같은 3차원 실수 공간은 3차원 벡터를 전부 모아둔 곳이고 이곳의 일부 벡터를 가지고 있는 것들이 부분 집합, subsapce입니다. supspace의 요소로 basis가 나옵니다. subspace를 전부 표현할 수 있는 벡터들을 basis라고 부릅니다. 즉 subspace의 재료벡터이면서 선형결합으로 subspace의 모든 벡터를 표현할 수 있다는 의미입니다. 하지만 선택된 재료벡터는 선형독립이여야 합니다. Find a basis 기저벡터(basis)는 unique하지 않기 때문에 한 subspace에 여러 개가 존재합니..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. 이번 강의에서는 선형종속(Linear dependence), 선형독립(Linear independence), 부분공간(subspace)를 배웁니다. 선형독립은 우리가 벡터 방정식으로 가능한 모든 조합(span)안에 상수벡터(target vector)가 들어가 있고 없고에 따라서 이 해가 특별한 해인지 아니면 수없이 많은지를 알게 해 준다고 했습니다. 해를 찾는 과정은 주어진 상수벡터에 가장 가깝거나 일치하는 벡터를 만들기 위해서 scale factor을 조절하는 것입니다. 여기서 해가 무수히 많이 존재한다는 것은 정답에 일치하는 벡터의 조합이 무수히 많은 것입니다. 이때를 선형종속이라고 합니다. 이러한 경우는 같은 차원의..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. 선형 결합은 $R^n$ 차원상의 벡터들에 상수 배를 곱해서 전부 더한 것입니다. 선형 결합이 나온 이유는 우리가 푸는 딥러닝 문제들도 입력 데이터에 상수 배(파라미터)를 곱하는 형태이기 때문입니다. 예제를 coulmn vector로 보면 $R^3$에 속하는 선형 결합으로 볼 수 있습니다. 그러면 다음과 같이 방정식 형태로 나오게 되는데 이것을 벡터 방정식이라고 합니다. Span 어떤 벡터들의 모든 선형 결합의 결과물을 모은 것이 Span입니다. 유한한 재료 벡터들을 가지고 만들 수 있는 모든 선형 벡터의 집합입니다. span은 하나의 실수 공간을 만들 수 있습니다. 연립 방정식이 아닌 벡터 방정식을 통해서 문제에 접근해보..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. Linear Equation(선형 방정식) $a_1x_1 + a_2x_2 + ... + a_nx_n $ 선형대수에서는 방정식을 한번에 생각할 수 있습니다. $[a_1, a_2 ... a_3]$ 일반적으로 Scalar를 표현할 때는 x 벡터를 표현할 땐 $x$ (굵게 씁니다.) Matrix를 표현할 땐 대문자로 $X$ Linear System: Set of Equations(방정식) Linear System은 선형 방정식(Linear Equations)의 집합! 연립 방정식을 의미합니다. 머신러닝에서도 data, feature의 target label들을 연립 방정식으로 푸는 것과 유사하게 계산합니다. (target lab..

본 내용은 edwith에서 인공지능을 위한 선형대수 내용 통해 작성되었습니다. 선형대수의 기본적 요소 Scalar 하나의 숫자 Vector 순서가 정해진 array 순서가 정해지지 않은 array는 set Matrix 행렬, 기본적으로 행렬은 2-dimensional array를 뜻합니다. Matrix의 사이즈는 = $row \times column$Row vector의 shape은 (1, n), Coulmn vector의 shape은 (n, 1)의 형태입니다. (Column은 기둥이라는 의미를 가집니다, 세로로 서있는 기둥을 생각하면 조금 더 구분하기 쉬워집니다.) Row vector을 Transpose 하면 Column vector가 나옵니다. Transpose는 아래 사진과 대각선을 중심으로 성분들..