ML, DL 정리 블로그

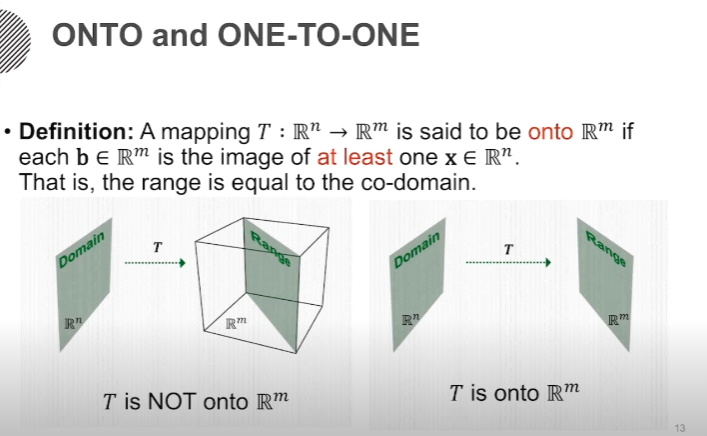
이번 강의에서는 임의의 행렬을 직교 기저(Orthogonal basis)를 가지는 행렬로 변환하는 그람 - 슈미트 직교화에 대해 배워보겠습니다. feature를 수직으로 바꿔주는 방법입니다. Gram - Schmidt Orthogonalization $ \left [ \begin{matrix} 3 \\ 6 \\ 0 \end{matrix} \right] \left [ \begin{matrix} 1 \\ 2 \\ 2 \end{matrix} \right] $ 두 벡터가 존재하는데 이 벡터의 내적은 $ 3 + 12 + 0 = 15$ 내적이 0이 아니니 두 벡터는 수직이 아닌 상태입니다. 그럼 그람 - 슈미트 직교화를 통해서 두 벡터를 수직으로 바꿔주겠습니다. 우선 두 벡터를 길이가 1인 벡터로 만듭니다. - v..

이전에 이어서 Orthogonal Projection에 대한 설명이 이어집니다. 마지막을 보면 otrhonormal한 U를 $UU^Tb$로 표기를 바꿔줬습니다. 즉 $b$를 $u_1, u_2$라는 orthonormal vector로 만들어지는 span 평면에 orthogonal projection 시킨 값을 구할 수 있는 또 다른 형태의 선형변환인 것입니다. 만약 $u_1, u_2$가 orthonormal 하다면 $y = \frac {y \dot u_1}{u_1 \cdot u_1} u_1 + \frac {y \dot u_2}{u_2 \cdot u_2} u_2$에서 밑항이 사라지게 됩니다. (길이가 1) 여기서 y가 아닌 b를 넣어주게 되면 $(u^T_1 b)u_1$에서 $u_1$을 행 벡터로 바꾸고 b와..

Orthogonal Projection은 $Ax = b$에서 b를 만족시키는 x를 구하지 못했을 때 근사한 $\hat {x}$로 $\hat{b}$을 구하기 위해서 사용됩니다. 이것을 행렬 곱으로 표현한다면 다음과 같습니다. - $\hat{b} = f(b) = A \hat{x} = A(A^TA)^{-1} A^Tb$ 즉 $A(A^TA)^{-1} A^T$을 $b$에 곱해서 Orthogonal Projection의 위치를 알아내는 것입니다. 주어진 차원에 벡터가 존재하고 그 벡터끼리 내적을 했을 때 전부 0이 나오면 그것을 Orthogonal set이라고 합니다. 즉 얻어낸 벡터가 전부 수직이라는 것입니다. 비슷하게 Orthonormal set 도 존재하는데 이것은 Orthogonal set에서 한 가지 조건을..

머신러닝에서 사용하는 gradient descent와 달리 normal equation은 최솟값을 직접 계산하는 방법입니다. $A^TAx = A^Tb$ $\hat{x} = (A^TA)^{-1}A^Tb$ 다음과 같이 역행렬이 존재한다면 가장 거리가 가까운 solution을 구할 수 있습니다. 여기서 x는 최단 거리의 수선의 발을 의미합니다. 그리고 x를 최단 거리의 벡터로 만들어주기 위해서 만족해야 할 식이 normal equation입니다. 정규 방정식도 일종의 선형 결합으로 우리가 방정식을 풀어서 x값을 구하게 된다면 그 값은 $x = arg \min \limits_{x} \| b-Ax \|$를 만족하게 됩니다. - 정확하게 $\|b - Ax\| = 0$으로 만들어주는 $x$값을 찾을 수 없으니 이 값..

이번 강의에서는 방정식의 개수가 미지수의 개수보다 많은 경우에 해결하는 방법에 대해서 이야기해줍니다. 다음과 같이 x를 근사하여 b값 차이(Error)를 구한 다음에 이 값들을 제곱의 합으로 나타냅니다. 제곱의 합이 적을수록 더 좋은 근삿값이 됩니다. 이러한 과정을 요약하자면 $\hat {x} = arg \min \limits_{x} \| b - Ax \|$가 됩니다. 최적의 x값 $\hat {x}$은 $b - Ax$ 값을 최소화시켜주는 x라는 의미입니다. - L2 norm을 최소화해주는 값을 찾는다. 이렇게 근사하는 방법은 b가 A의 span에 포함되지 않을 때 b를 A의 span 평면에 orthogonal projection 한 값을 찾는 것입니다. - 이렇게 하면 A가 이루는 평면에서 b값과 가장 ..

- 본 내용은 edwith의 인공지능을 위한 선형대수 강의를 통해 작성되었습니다. 이번 학습의 목표는 Least Squares Ploblem에 대한 개념을 이해하는 것 입입니다. 벡터와 관련된 이 개념들은 선형대수에서 중요한 개념이니 알아두면 좋습니다. 핵심 키워드 내적(Inner Product, Dot Product) 벡터의 길이(Vector Norm) 단위벡터(Unit Vector) 직교벡터(Orthogonal Vectors) Leaset Squares = 선형 방정식을 다루는 상황에서 방정식의 개수가 미지수의 개수보다 많은 상황일 때를 말합니다. - feature의 개수보다 데이터 개수가 더 많을 때 방정식이 3개이고 미지수가 3개인 이 상태에서 데이터를 더 수집한다면 방정식의 개수가 늘어나게 됩니..

전사함수와 일대일 함수 (ONTO and ONE - TO - ONE) ONTO ONTO는 공역(입력) = 치역(출력이 될 수 있는 애들)일 때 이 경우를 ONTO라고 부릅니다. 공역과 치역이 같을 때! 공역과 치역이 같을 때 필요한 최소한의 조건은 정의역이 치역 이상이어야 합니다. 즉 치역의 모든 원소를 한번 이상의 매핑이 필요합니다. 1. $R^3 \rightarrow R^2$ 2. $R^2 \rightarrow R^3$ 2번째의 경우에는 절대 전사함수가 될 수 없습니다. 위에서 말한 최소한의 조건을 만족시키지 못했기 때문입니다. - 입력 Dimention이 출력 Dimention보다 작으면 안 됩니다. $T ( \left [ \begin{matrix} 1 \\ 0 \end{matrix} \right]..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. 선형변환은 신경망에서 가장 기초적인 형태입니다. 선형변환에서 일어나는 일은 결과에 따라 Standard vector값이 바뀌면서 좌표도 바뀌게 됩니다. $[1, 0], [0, 1]$이였던 벡터가 선형변환을 통해서 $[2, 3]$과 같은 형태로 바뀌고 그에 따라 좌표도 변경된 것입니다. - 선형변환을 기하학적으로 표현한 것! 이 사진에서는 56, 231, 24, 2 값을 가지는 이미지가 벡터화가 돼서 입력층으로 들어갑니다. 이 구조가 이전 게시물에서 말했던 fully connected layer의 모습입니다. 옆에 $(3 \times 4)$ 행렬과 $(4 \times 1)$ 벡터가 있는데 여기서 행렬은 3차원으로 shape..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. 함수의 입력으로 쓰이는 모든 집합은 정의역(domain), 함수의 출력값으로 쓰이는 모든 output의 집합은 공역(co-domain), 입력에 대한 출력값은 image라고 합니다. range는 치역으로 실제로 사용된 공역입니다. ex) $2x$라는 함수가 있을 때 $x = 1$의 image는 2 선형변환의 조건 $T(cu + dv) = cT(u) + dT(v)$을 만족할 때 ($u, v$는 벡터입니다.) $3x$와 같은 단순 상수배이면 선형변환이 됩니다. $y = 3x + 2$와 같이 bias가 포함되면 선형변환이 아닙니다. 위 조건을 만족시키지 않기 때문입니다. 하지만 이러한 경우도 수정을 해주면 선형변환이라고 할 수..

- 본 내용은 edwith에서 인공지능을 위한 선형대수 내용을 통해 작성되었습니다. subspace는 부분공간, 부분집합으로 생각하시면 됩니다. span과 유사한 개념입니다. $R^3$같은 3차원 실수 공간은 3차원 벡터를 전부 모아둔 곳이고 이곳의 일부 벡터를 가지고 있는 것들이 부분 집합, subsapce입니다. supspace의 요소로 basis가 나옵니다. subspace를 전부 표현할 수 있는 벡터들을 basis라고 부릅니다. 즉 subspace의 재료벡터이면서 선형결합으로 subspace의 모든 벡터를 표현할 수 있다는 의미입니다. 하지만 선택된 재료벡터는 선형독립이여야 합니다. Find a basis 기저벡터(basis)는 unique하지 않기 때문에 한 subspace에 여러 개가 존재합니..