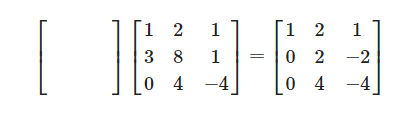ML, DL 정리 블로그

치환행렬 (Permuation matrix)은 P라고 표기하며 행 교환을 해줍니다. $PA = LU$ 행 교환이 이루지는 행렬에 대한 소거를 배워보겠습니다. P는 재정렬된 행이 있는 단위행렬입니다. 행을 교환할 수 있는 가짓수는 몇 개가 있을까요? 팩토리얼로 나타낼 수 있습니다. $n! = n(n-1) + ... + 2 + 1$ 이렇게 $n \times n$ 치환의 재정렬 가짓수를 계산할 수 있습니다. 치환행렬의 특징은 $P^{-1} = P^T$ 전치하면 역행렬을 구할 수 있어서 우리가 바꿨던 행들을 다시 원래대로 복구할 수 있습니다. 대칭행렬 (Symmetric matrices) 이 행렬은 전치를 통해서 행렬이 바뀌지 않습니다. 어떻게 하면 대칭행렬을 얻을 수 있을까요? 다음과 같은 rectangula..

저번 강의에서 우리는 소거를 통해 A행렬이 소거가 완료된 행렬 U로 이동한다는 것을 배웠습니다. 이번 시간에는 두 개의 연산을 진행하는 행렬을 소거해보겠습니다. $AB$의 역행렬을 구해봅시다. 개별적인 두 행렬의 역행렬을 구해야 합니다. 그리고 그 두 역행렬을 곱해야 하는데 곱하는 순서가 있습니다. 바로 역순으로 곱해줘야 합니다. $ABB^{-1}A^{-1} = AB(AB)^{-1}$ $A(BB^{-1})A^{-1} = AIA^{-1} = AA^{-1} = I$ 이렇게 역순으로 곱하게 되면 A와 A의 역행렬을 곱할 수 있게 됩니다. LU decomposition LU 분해는 행렬의 가장 기본적인 분해입니다. $A = LU$ 여기서 U는 A에 소거를 진행한 결과물입니다. 설명을 위해 행렬 A이 존재한다고 ..

행렬 곱셈에 대한 규칙을 논의해보겠습니다. 1. Matrix multiplication 2. Inverse of $A$ $AB$ $A^T$ 3. Gauss - Jordan 행렬 곱셈에 대해 조금 더 알아보고 gauss - jordan을 사용하여 역행렬을 구하는 방법에 대해 알아보겠습니다. 행렬 곱셈에는 몇 가지 방법이 있는데 우선 $row \times column$에 대해 알아보겠습니다. 1. 행렬을 곱하는 방법 $row \times column$ 다음과 같은 행렬 연산이 있다고 해봅시다. ($AB = C$) $\left[\begin{matrix} & & & \\ & & & \\ a_{31} & a_{32} & a_{33} & a_{34} \end{matrix} \right] \left[\begin{ma..

방정식을 푸는 방법들은 다양합니다. 1. Elimination (소거법) - Success - Failure 2. Back-substitution (후방 대입법) 3. Elimination matrices (소거 행렬) 4. Matrix multiplication (행렬 곱) 여기서 소거법은 모든 소프트웨어 패키지가 방정식을 풀 때 사용하는 방법입니다. - 소거법이 성공하면 solution을 얻습니다. - 좋은 matrix에 대해서만 소거법을 진행했을 때 solution을 얻을 수 있습니다. (square matrix가 아닌 것도 solution을 얻을 수 있습니다.) $ x + 2y + z = 2 $ $ 3x + 8y + z = 12 $ $ 4y + z = 2 $ 다음과 같이 3개의 방정식과 3개의 미..

다음과 같이 두 개의 미지수를 가진 두 개의 방정식이 존재한다고 해봅시다. $2x - y = 0$ $-x + 2y = 3$ 이 두 방정식을 행렬로 표현한다면 각각의 계수와 미지수를 따로 묶어서 표현합니다. $$ \left[\begin{matrix} 2 & -1 \\ -1 & 2 \\ \end{matrix} \right] \left[\begin{matrix} x \\ y \\ \end{matrix} \right] = \left[\begin{matrix} 0 \\ 3 \\ \end{matrix} \right]$$ 방정식의 계수를 모아둔 행렬을 계수 행렬(coefficient matrix)이라고 부르고 $A$로 표기합니다. 그다음 미지수 벡터(the vector of unknown) 를 $x$ 마지막으로 이 ..

Orthogonalization이 가능한 상태를 생각해봅시다. n개의 선형독립적인 Eigenvector를 사용할 수 있는 상황에서, 다음과 같이 $D = V^{-1}AV$에서 $D$에도 $V$, $V^{-1}$ 그리고 $A$에도 $V$, $V^{-1}$을 곱합니다. Diagonal 하다는 것은 V의 역행렬이 존재한다는 것입니다. $VDV^{-1} = AV^{-1}VV{-1}V$ $VDV^{-1} = A$ - 다음과 같이 나오게 됩니다. 이것을 고유값 분해(Eigendecomposition)이라고 합니다. 주어진 matrix를 여러 matrix의 곱으로 나타내는 것을 matrix에 대한 decomposition이라고 말합니다. 이 분해를 하기 위한 조건으로 V는 invertible 한 matrix이어야 합..

대각화란 주어진 행렬을 대각행렬로 만드는 것을 말합니다. 기본적으로 square matrix를 사용합니다. $D = V^{-1}AV$ A라는 matrix에 V와 V의 역행렬을 곱해주어 대각 성분만 남게 만듭니다. 이 방법은 항상 가능한 것이 아니라 상황에 따라 달라집니다. 위에 식을 만족시키는 V를 찾을 수 있는 경우에만 대각화가 가능합니다. V의 shape은 A의 shape과 동일합니다. $VD = AV$란 식을 얻었습니다. A가 (3, 3) 행렬이라고 할 때 V도 (3, 3) 행렬이 됩니다. $AV_1 = \lambda V_1...$ 여기서 $V$를 Eigenvector $\lambda$를 Eigenvalue로 생각해보면 이전에 배웠던 Eigenvalue, Eigenvector가 만족해야 하는 식과 ..

이번 강의에서는 지난 시간에 배운 새로운 벡터 공간의 개념을 바탕으로 고유벡터와 고유값을 더 이해하고 특성 방정식(Characteristic Equation)을 통해 이들을 구하는 법을 알아봅시다. Eigenvector와 Eigenvalue를 만족시키는 기본적인 식이 $(A - \lambda I)x = 0$ 입니다. $\lambda$ 정해졌다면 위에 식에 대한 Null space를 찾으면 그것이 $x$입니다. 다음과 같이 $A - \lambda I$를 뺏는데 나온 행렬의 차원을 보면 Row 차원의 벡터들이 중복되어 있어서 벡터들로 만들 수 있는 것은 선 하나입니다. 여기서 Eigenvalue는 3으로 사용했습니다. 3을 사용해서 Lineary independent하게 만들어 줬습니다. 여기서 Row 벡터..

Null space는 $Ax = 0$을 만족시키는 $x$들의 집합을 Null space of A라고 합니다. - Rectangular matrix에도 적용이 가능합니다. $ \left [ \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix} \right] \left [ \begin{matrix} x \\ y \end{matrix} \right] = \left [ \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \right]$ 다음과 같이 행렬 연산을 했을 때 0이 나오게하는 column vector를 찾아야 합니다. (행렬에 대해 수직인 x, y) 다음과 같이 $a^T$들과 내적했을 때 전부 0이 나오는 수직인 x를 찾고 모아둔 것이 Null..

고유값 분해는 주성분 분석(PCA: Principal Component Analysis)에서 자주 쓰이는 개념입니다. 이번 강의에서 고유값 분해를 배우기 위한 첫 단계인 고유 벡터와 고유값의 개념에 대해 배워보도록 하겠습니다. identity composition - 주어진 행렬에 대해 굉장히 중요한 정보를 추출하는 과정입니다. - Square matrix의 Eigenvector가 non - zero 적어도 하나의 원소가 아닌 벡터일 때 다음 식을 만족해야 합니다. $Ax = \lambda x$ 다음과 같이$3 \times 3$ square matrix와 3차원 벡터 x의 곱과 스칼라와 x 벡터의 곱이 같아야 합니다. 이러한 조건을 만족시키는 벡터 x를 A 행렬의 Eigenvector라고 합니다. $\l..