이번 강의에서도 선형 방정식을 푸는 방법에 대해 배워보겠습니다.
$Ax = b$
$x_1 + 2x_2 + 2x_3 + 2x_4 = b_1$
$2x_1 + 4x_2 + 6x_3 + 8x_4 = b_2$
$3x_1 + 6x_2 + 8x_3 + 10x_4 = b_3$
이전 강의에서 사용한 matrix인데 다음과 같이 방정식으로 풀어뒀습니다. 1, 2행을 더하면 3행이 나오는 행렬입니다. 이 행렬의 솔루션이 존재하는지 알아보겠습니다.
이 시스템에서 솔루션을 갖기 위해서는 $b_1, b_2, b_3$이 갖춰야 할 조건이 존재합니다.
만약 $b_1 = 1$ 그리고 $b_2 = 5$이라면 $b_3$는 6이 됩니다.
- 그 이유는 첫 번째 두 번째 식을 더 했을 때 세 번째 식이 나오니 우변을 보면 $b_3 = b_1 + b_2$ 꼴이 됩니다. 이 조건이 맞아야지 해가 존재하는 것이고 이 값과 다르다면 저 방정식을 만족시키는 해를 찾을 수 없습니다.
조건을 소거법으로 어떻게 발견하는지 알아봅시다.
$\left[\begin{matrix} 1 & 2 & 2 & 2 & b_1 \\ 2 & 4 & 6 & 8 & b_2 \\ 3 & 6 & 8 & 10 & b_3 \end{matrix} \right] $
다음과 같이 Augmentation matrix로 만들어 준 뒤 소거를 진행하면
$\left[\begin{matrix} 1 & 2 & 2 & 2 & b_1 \\ 0 & 0 & 2 & 4 & b_2 - 2b_1 \\ 0 & 0 & 2 & 4 & b_2 - 3b_1 \end{matrix} \right] $
중간 과정이 이렇게 되고 2번째 행을 3번째 행에 빼주면
$\left[\begin{matrix} 1 & 2 & 2 & 2 & b_1 \\ 0 & 0 & 2 & 4 & b_2 - 2b_1 \\ 0 & 0 & 0 & 0 & b_3 - b_2 - b_1 \end{matrix} \right] $
전부 0이 돼버립니다. 마지막 방정식을 봐보면 $0 = b_3 - b_2 - b_1$이 됩니다. 이 조건이 성립할 때 솔루션이 존재하게 됩니다.
b값들을 모아둬서 보면
$b = \left[\begin{matrix} 1 \\ 5 \\ 6 \end{matrix} \right] $
$\left[\begin{matrix} b_1 \\ b_2 - b_1 \\ b_3 - b_2 - b_1 \end{matrix} \right] = \left[\begin{matrix} 1 \\ 3 \\ 0 \end{matrix} \right]$
미지수가 4개고 방정식이 3개지만 3번째 방정식은 없는 거나 마찬가지라서 이렇게 2개의 방정식으로 4개의 미지수를 풀어 봤습니다.
Solvability
여기서 말하는 해결 가능성(Solvability)은 $Ax = b$에 대한 것입니다.
어떤 방식으로 x를 찾아야 할까요?
1. 모든 자유 변수를 0으로 설정하고 푸는 것이 가장 편리한 방법입니다. (particular solution, 특수해)
- 그다음 피벗 변수에 대해 $Ax = b$를 풉니다.
- 자유 변수가 0인 솔루션이 생기게 됩니다.
2. $Ax = 0$에 대한 솔루션을 구하면 됩니다. (null space solution)
이렇게 $Ax = b$일 때와 $Ax = 0$일 때의 $x$ 값들을 각각 $x_p, x_n$이라고 하겠습니다.. 이렇게 찾은 솔루션을 더해주면 완전해(complete solution)을 얻을 수 있습니다.
$x = x_p + x_n$
$Ax_p = b$
$Ax_n = 0$
$A(x_p + x_n) = b$
- b가 A의 span에 존재한다면 솔루션을 찾을 수 있습니다. 그리고 이 상황에서 $Ax = b$의 해와 $Ax = 0$의 해를 더해도 우변이 b가 나오기 때문에 완전해를 부분 공간의 합으로 표현할 수 있습니다.
하지만 $x_p + x_n$은 원래 원점을 포함하는 null space가 $x_p$만큼 이동하게 되므로 더 이상 원점을 지나지 않고 $x_p$를 지나기 때문에 부분 공간으로 볼 수 없습니다.
Rank
행렬에 m개의 행이 있고 r개의 피벗이 있을 때 이 둘은 어떤 관계를 가지고 있을까요?
- r은 m보다 항상 작거나 같습니다. m개 이상의 피벗을 가질 수 없습니다. ($r \le m$)
- n개의 열이 있을 때 n의 길이가 피벗을 정하는데 영향을 줍니다, 그렇기에 r은 n보다도 작거나 같습니다. ($r \le n$)
- r = n 이면 free column이 없습니다, 이 경우 null space 솔루션은 영벡터만 존재합니다.
- pivot column은 특정한 솔루션 차원에 존재하고 free column은 null space에 존재합니다.
$A = \left[\begin{matrix} 1 & 3 \\ 2 & 1 \\ 6 & 1 \\ 5 & 1\end{matrix} \right] $
다음과 같은 행렬이 존재할 때 피벗의 개수는 2개, 선형독립으로 null space에 영벡터만 존재합니다.
- r = m < n 일 때 소거된 행렬에서 남아있는 부분이 free column

- r = m = n 일때 소거된 행렬은 항등 행렬이 된다.
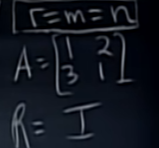
각각의 r, m, n 관계와 솔루션의 수

요약
- 소거법을 통해서 $Ax$ 문제를 해결할 수 있는 범위를 찾을 수 있다.
- $Ax = b$ 문제를 해결할 때 free column은 전부 0으로 설정하고 pivot column에 대해서만 풀면 특수해를 얻고 그 다음 $Ax = 0$에 대해 해결하면 null space해를 얻을 수 있다. 마지막으로 두 개를 조합하면 $Ax = b$에 대한 해를 더 얻을 수 있다.
- 이때 두 해를 더하면서 null space가 특수해 만큼 이동을하여 원점을 포함하지 않게 되버리므로 완전해는 부분 공간으로 볼 수 없다. (부분 공간의 합으로 표현이 가능하지만 부분 공간이 아니다.)
- rank는 pivot보다 항상 크거나 같다, column도 pivot보다 항상 크거나 같다.
-
'수학 > Gilbert Strang Linear Algebra' 카테고리의 다른 글
| 10. The Four Fundamental Subspaces (0) | 2022.02.16 |
|---|---|
| 9. Independence, Basis and Dimension (0) | 2022.02.11 |
| 7. 선형방정식(Solving Ax = 0: Pivot Variables, Special Solutions) (0) | 2022.02.06 |
| 6. 열공간과 영공간(Column Space and Nullspace) (2) | 2022.01.27 |
| 5. 전치행렬, 치환행렬, 벡터 공간(Transposes, Permutations, Spaces R^n) (0) | 2022.01.26 |