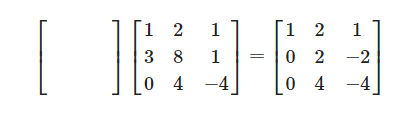3차원 벡터라면 어떻게든 3차원 공간 안에 존재합니다. $R^3$의 부분공간은 다음과 같이 원점을 가지는 평면과 원점을 지나는 직선입니다. 평면을 P, 직선을 L이라고 하겠습니다. 그러면 $P \cup L$도 부분공간에 해당할까요? (아니요) - 선형결합의 규칙이 성립되지 않습니다. 임의의 상수를 곱하거나 공간 내의 다른 원소끼리 더해도 같은 공간에 존재해야 하는데, 각자 다른 공간에 있는 것들도 합친 것이기 때문에 불가능합니다. - 만약 직선이 평면 위에 존재하다면 가능할 것입니다. 이 경우 선형결합과 벡터 덧셈, 스칼라 곱을 해도 같은 벡터 공간에 존재하기 때문입니다. 사진속 평면과 직선은 원점만 공유하게 됩니다. 서로 다른 공간에 존재하지만 원점은 똑같이 지나갑니다. 여기 한 행렬이 있습니다. 이 ..